CIRCUITOS EN SERIE Y EN PARALELO
En esta ocasión te vamos a explicar los circuitos en serie y en paralelo en corriente continua con métodos profesionales de análisis.
También verás que hay enlaces para aprender a calcular los circuitos mixtos y los de corriente alterna.
También se supone que conoces las Magnitudes Eléctricas de tensión, intensidad y resistencia.
Por último y antes de empezar, te recomendamos el siguiente libro para aprender los principios básico de la electricidad y el cálculo de circuitos eléctricos, tanto de corriente contínua como de alterna:
O hacer el curso en UDEMY para aprender a resolver circuitos de corriente contínua
Índice de Contenidos:
- Fundamentos del Análisis de Circuitos
- Circuitos en Serie
- Ejercicios Circuitos en Serie
- Circuitos en Paralelo
- Ejercicios Circuitos en Paralelo
- Comparativa Serie vs Paralelo
- Métodos Avanzados de Análisis
- Circuitos Mixtos
- Circuitos en Corriente Alterna
Fundamentos del Análisis de Circuitos Eléctricos
El análisis de circuitos eléctricos se basa en leyes fundamentales que rigen el comportamiento de la corriente eléctrica y el voltaje. Comprender estas leyes es esencial antes de abordar circuitos más complejos.
La Ley de Ohm: Fundamento del Cálculo
La Ley de Ohm establece la relación fundamental entre voltaje (V), corriente (I) y resistencia (R) en cualquier elemento del circuito:
Voltaje (V) = Intensidad (A) × Resistencia (Ω)
De esta fórmula principal se derivan las otras dos formas:
- I = V / R → Para calcular la intensidad de corriente
- R = V / I → Para calcular la resistencia
Potencia Eléctrica en Circuitos
La potencia eléctrica (P) representa la tasa de energía consumida o disipada en un circuito. Se mide en Vatios (W) y se calcula mediante:
Potencia (W) = Voltaje (V) × Intensidad (A)
Fórmulas alternativas combinando con la Ley de Ohm:
- P = I² × R → Útil cuando conoces intensidad y resistencia
- P = V² / R → Útil cuando conoces voltaje y resistencia
Principio fundamental: En cualquier circuito (serie, paralelo o mixto), la suma de las potencias individuales siempre es igual a la potencia total: Pt = P1 + P2 + P3 + ...
Circuitos en Serie
Los circuitos en serie son configuraciones donde los componentes se conectan uno detrás de otro, formando un único camino para la corriente eléctrica.
Características Fundamentales de los Circuitos en Serie
Veamos una bombilla y un timbre conectados en serie:
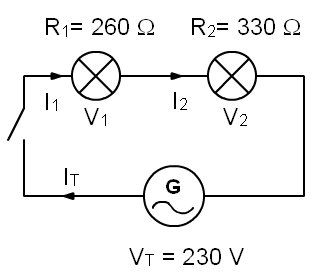
Fíjate que la intensidad que sale de la pila es la misma que atraviesa cada receptor:
Resistencia Equivalente en Serie
La resistencia equivalente (también llamada resistencia total) es una resistencia única que puede sustituir a todas las resistencias en serie sin cambiar el comportamiento del circuito.
Veamos como se resuelve un circuito en serie con 3 resistencias:
Ejercicios de Circuitos en Serie Resueltos
Lo primero será calcular la resistencia total o resistencia equivalente porque podemos sustituir todas las resistencias de los receptores en serie por una sola cuyo valor será el de la resistencia total.
Fíjate en el circuito siguiente:
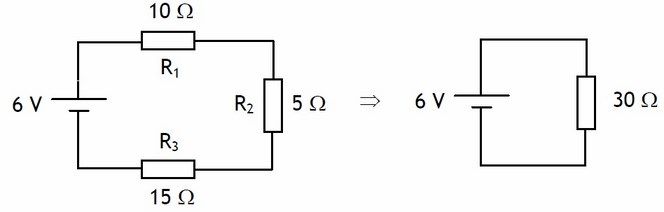
Rt = R1 + R2 + R3 = 10 + 5 + 15 = 30Ω
El circuito equivalente quedaría con una sola resistencia de 30 ohmios.
Según la ley de ohm:
It = Vt / Rt = 6 / 30 = 0,2 A
Como todas las intensidades en serie son iguales:
It = I1 = I2 = I3 = 0,2A (Todas valen 0,2 amperios)
Aplicamos la ley de ohm en cada receptor:
V1 = I1 × R1 = 0,2 × 10 = 2V
V2 = I2 × R2 = 0,2 × 5 = 1V
V3 = I3 × R3 = 0,2 × 15 = 3V
Comprobamos si efectivamente las suma de las tensiones es igual a la tensión total:
Vt = V1 + V2 + V3 = 2 + 1 + 3 = 6 V ✓ Correcto
Como ves ya tenemos todos los datos del circuito, por lo tanto ¡Ya tenemos resuelto nuestro circuito en serie!
Cálculo de Potencias en Serie
Puede que nos pidan calcular las potencias en el circuito. Sabiendo la fórmula de la potencia que es P = V × I:
P1 = V1 × I1 = 2 × 0,2 = 0,4w
P2 = V2 × I2 = 1 × 0,2 = 0,2w
P3 = V3 × I3 = 3 × 0,2 = 0,6w
Fíjate que la suma de las potencias de cada receptor siempre es igual a la potencia total (en serie y en paralelo):
Pt = P1 + P2 + P3 = 0,4 + 0,2 + 0,6 = 1,2w ✓
Cálculo de Energía Consumida
Si nos piden la energía consumida en un tiempo determinado aplicamos la fórmula: E = P × t
Por ejemplo para 2 horas:
- Et = Pt × t = 1,2 × 2 = 2,4 Wh (vatios por hora)
Si nos piden en Kwh (kilovatios por hora) antes de aplicar la fórmula tendremos que pasar los vatios de potencia a kilovatios dividiendo entre mil:
- Pt = 0,0012 Kw
- Et = 0,0012 × 2 = 0,0024 Kwh
Aquí tienes otros dos circuitos en serie resueltos:
Ojo que no te despiste la colocación de las resistencias en el segundo circuito, si te fijas están una a continuación de otra, por lo tanto están en serie.
Para circuitos en serie en corriente alterna visita este enlace: Circuitos Corriente Alterna
Circuitos en Paralelo
Los circuitos en paralelo son configuraciones donde los componentes comparten sus puntos de conexión, creando múltiples caminos para la corriente eléctrica.
Características Fundamentales de los Circuitos en Paralelo
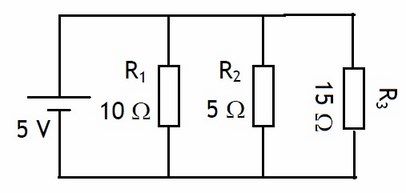
OJO no te confundas, si te fijas es al revés que en serie.
O despejando: Rt = 1 / (1/R1 + 1/R2 + 1/R3 + ...)
Fórmula simplificada para dos resistencias en paralelo:
"Producto dividido por suma"
Ejercicios de Circuitos en Paralelo Resueltos
Vamos a calcular un circuito en paralelo. Podríamos seguir los mismos pasos que en serie (primero resistencia equivalente, luego la It, etc.), pero en este caso vamos a seguir otros pasos y nos evitaremos tener que utilizar la fórmula de la resistencia total.

Sabemos que todas las tensiones son iguales en paralelo:
Vt = V1 = V2 = V3 = 5V (todas valen 5 voltios)
Aplicamos la ley de ohm (I = V / R) en cada receptor:
I1 = V1 / R1 = 5 / 10 = 0,5A
I2 = V2 / R2 = 5 / 5 = 1A
I3 = V3 / R3 = 5 / 15 = 0,33A
La intensidad total del circuito será la suma de todas las de los receptores:
It = I1 + I2 + I3 = 0,5 + 1 + 0,33 = 1,83A
(Nota: I3 realmente es 0,333333... por lo que cometeremos un pequeño error sumando solo 0,33, pero es tan pequeño que no pasa nada)
Para calcular las potencias y las energías se hace de la misma forma que en serie.
Aquí te dejamos otro circuito en paralelo resuelto:
Comparativa Completa: Serie vs Paralelo
Esta tabla resumen te ayudará a identificar rápidamente las diferencias entre ambos tipos de circuitos:
| Característica | Circuitos en Serie | Circuitos en Paralelo |
|---|---|---|
| Conexión | Un camino único, componentes uno tras otro | Múltiples caminos, componentes comparten nodos |
| Intensidad (I) | It = I1 = I2 = I3 (igual en todos) | It = I1 + I2 + I3 (se suma) |
| Voltaje (V) | Vt = V1 + V2 + V3 (se suma) | Vt = V1 = V2 = V3 (igual en todos) |
| Resistencia Total | Rt = R1 + R2 + R3 | 1/Rt = 1/R1 + 1/R2 + 1/R3 |
| Potencia Total | Pt = P1 + P2 + P3 (en ambos casos) | Pt = P1 + P2 + P3 (en ambos casos) |
| Si falla un componente | ❌ Todo el circuito deja de funcionar | ✓ Los demás componentes siguen funcionando |
| Aplicación típica | Luces navideñas antiguas, fusibles | Instalaciones domésticas, enchufes |
| Rt comparada con resistencias individuales | Rt es MAYOR que cualquier resistencia individual | Rt es MENOR que la resistencia más pequeña |
Métodos Avanzados de Análisis de Circuitos
Para circuitos más complejos que combinan elementos en serie y paralelo, existen métodos sistemáticos profesionales que facilitan el análisis:
1. Método "Descomponer y Reconstruir" (Break-Down Build-Up)
Este es el método más utilizado en la industria para analizar circuitos eléctricos complejos:
- Redibuja el circuito en forma lineal para identificar claramente relaciones serie/paralelo
- Combina resistencias usando fórmulas de resistencia equivalente
- Redibuja nuevamente simplificando hasta obtener una sola resistencia total
- Aplica la Ley de Ohm para determinar la corriente total del circuito
- Retrocede paso a paso por los dibujos anteriores
- Determina voltaje y corriente en cada resistor usando la Ley de Ohm
- Verifica que la suma de potencias coincida con la potencia total
2. Leyes de Kirchhoff para Circuitos Complejos
Las Leyes de Kirchhoff son fundamentales para analizar circuitos que no se pueden simplificar fácilmente:
En cualquier nodo (punto de unión) de un circuito, la suma de corrientes que entran es igual a la suma de corrientes que salen.
Σ Ientrada = Σ Isalida
En cualquier lazo cerrado de un circuito, la suma algebraica de todas las tensiones es igual a cero.
Σ V = 0
(La suma de subidas de voltaje = suma de caídas de voltaje)
Aplicación Práctica de las Leyes de Kirchhoff
Para aplicar estas leyes en circuitos complejos:
- Asigna direcciones a las corrientes: Aunque no sepas la dirección real, asigna una arbitrariamente. Si el resultado es negativo, simplemente significa que la dirección real es opuesta.
- Identifica todos los nodos y lazos: Los nodos son puntos donde se conectan tres o más elementos. Los lazos son caminos cerrados.
- Escribe ecuaciones KCL para cada nodo: Excepto uno (ya que sería redundante).
- Escribe ecuaciones KVL para lazos independientes: Recorre cada lazo sumando algebraicamente los voltajes.
- Resuelve el sistema de ecuaciones: Usa álgebra lineal o métodos numéricos para encontrar las corrientes desconocidas.
Si tenemos un lazo con una fuente de 12V y tres resistores (R1=10Ω, R2=20Ω, R3=30Ω) en serie:
+12V - I×R1 - I×R2 - I×R3 = 0
12 - I×10 - I×20 - I×30 = 0
12 = I×60
I = 0,2A
3. Método de Análisis Nodal
El análisis nodal es especialmente útil para circuitos con múltiples fuentes de voltaje:
- Selecciona un nodo de referencia (tierra, 0V)
- Asigna voltajes a todos los demás nodos respecto a la referencia
- Aplica KCL en cada nodo no referencia
- Expresa cada corriente en términos de los voltajes nodales usando Ley de Ohm
- Resuelve el sistema de ecuaciones resultante
4. Método de Análisis de Mallas
El análisis de mallas es ideal para circuitos planos con múltiples lazos:
- Identifica todas las mallas (lazos que no contienen otros lazos)
- Asigna una corriente de malla a cada una
- Aplica KVL a cada malla
- Resuelve el sistema de ecuaciones para encontrar las corrientes de malla
- Las corrientes reales en las ramas se obtienen por superposición de las corrientes de malla
Para saber más sobre las leyes de Kirchhoff pincha en el enlace en rojo.
Simplificación mediante Equivalentes de Thévenin y Norton
Para circuitos complejos, podemos simplificar partes usando los teoremas de Thévenin y Norton:
- Teorema de Thévenin: Cualquier circuito lineal con dos terminales puede representarse como una fuente de voltaje (Vth) en serie con una resistencia (Rth)
- Teorema de Norton: El mismo circuito puede representarse como una fuente de corriente (In) en paralelo con una resistencia (Rn)
Estos teoremas son especialmente útiles cuando analizas el efecto de conectar diferentes cargas a un circuito complejo.
Si quieres aprender estos 2 teoremos visita: Teorema de Thevenin y de Norton
Circuitos Mixtos
Para calcular circuitos mixtos (mezcla de serie y paralelo con 3 o más resistencias), te recomendamos que vayas al siguiente enlace: Calculo de Circuitos Mixtos
Circuitos en Corriente Alterna
Si quieres aprender a calcular circuitos en Serie en corriente alterna te dejamos este otro enlace:
Y el fantástico libro con ejercicios para aprender a calcular circuitos en serie, paralelo y mixtos tanto en contínua como en corriente alterna: Libro Circuitos Eléctricos
Si te ha gustado Circuitos en Serie y Paralelo haz click en Compartir, Gracias:
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
TAMBIÉN TE PUEDE INTERESAR
Resistencia Eléctrica
Resistencia Equivalente
Código de Colores de Resistencias
Tipos de Conexiones Eléctricas
Leyes de la Electricidad y Ley de Ohm
Ejercicios de Potencia Eléctrica
Circuitos Eléctricos
Potencia Eléctrica
Cálculo de Circuitos Mixtos
Cálculos Circuitos de Una Lámpara
Condensador Eléctrico
Voltímetro
Amperímetro
Herramientas Eléctricas
Instalación Eléctrica en Viviendas
