KARNAUGH SIMPLIFICACIÓN DE FUNCIONES

En 1953 el Ingeniero Maurice Karnaugh ideó un método de que permitía minimizar funciones lógicas mediante la confección de tablas o mapas del estado de sus variables.

El método de simplificación de Karnaugh es recomendable utilizarlo para sistemas con un número de variables de entrada comprendidas entre 2 y 5 variables.

Para aplicar la simplificación de la función lógica por karnaugh primero es necesario realizar la tabla de la verdad del problema o tener la función lógica del circuito a simplificar.

Una vez tenemos la tabla o función lógica es cuando aplicamos la simplificación por el método de karnaugh.

Si no sabes obtener la tabla de la verdad y la función lógica entonces primero vete al siguiente enlace: Electrónica Digital.

Aquí partimos teniendo en cuenta que estos conocimientos ya los tienes o que te las dan para resolver el problema.

Pasos Para la Simplificación de la Ecuación o Función Lógica

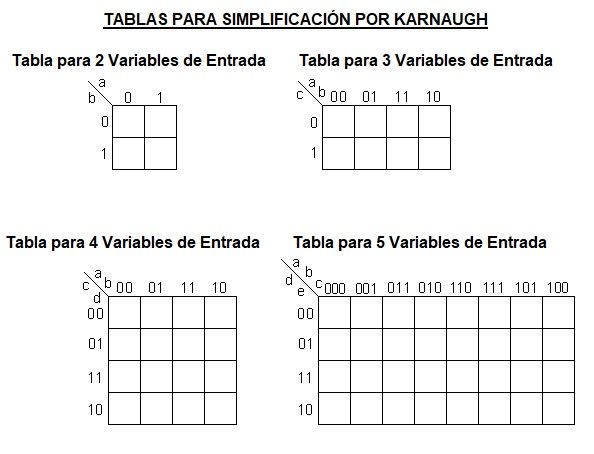
1º) Dibujamos un tabla de karnaugh con tantas casillas como 2ⁿ , siendo "n" el número de variables.

Por ejemplo para 2 variables la tabla tendrá 4 casillas, para 3 variables tendrá 8 casillas y para 4 variables tendrá 16 casillas.

No se recomienda este método para más de 4 variables.

A continuación puedes ver como quedarían las tablas en función del número de variables de entrada.



2º) Lo que pretendemos con esta tabla es tener una tabla con todos los estados de la salida (0 o 1) para las diferentes combinaciones de las variables de entrada.

El valor de la salida de cada cuadrado lo sacaremos de la tabla de la verdad que ya tendremos que tener.

Imagina que una tabla de la verdad de 2 variables nos dice que para a = 0; b = 1 la salida es 1, pues construiremos una tabla de 2 variables como la primera de arriba y en el cuadro correspondiente a= 0 y b = 1 pondremos el valor de 1 (cuadro de la primera fila el segundo de la derecha del todo)

Por ejemplo, en la tabla para 3 variables, ponemos las variables a y b encima de la línea del vértice superior (columnas), y en las columnas de la tabla tenemos las posibles combinaciones de esas 2 variables: 00, 01, 11 o 10.

En la parte de abajo (filas) ponemos la otra variable que nos queda, la variable c, y sus posibles estados en cada fila que pueden ser 0 o 1.

¡¡¡OJO!!! es Muy Importante que los ceros y unos de cada variable estén en el orden que aparecen en las tablas de arriba.

Por ejemplo, en la segunda tabla, para 3 variables, los valores de las variables "ab" NO se deben poner en este orden 00, 01, 10 y 11 aunque parezca el más lógico.

OJO Esto es un error muy frecuente entre los alumnos.

El orden correcto es 00, 01, 11 y 10. Primero 11 y luego 10.

¿Por qué este orden? Porque es obligatorio que al pasar de una combinación a otra en la tabla solo cambie el valor de una de las variables.

Por ejemplo, si pasáramos de la segunda columna de 01 a la tercera con valores 10, cambiaría el estado de las dos variables.

La variable a sería en la primera combinación 0 (01) y en la segunda sería 1 (10), luego "a" cambiaría, pero b también cambiaría ya que sería en la primera 1 (01) y en la segunda 0 (10).

Sin embargo, si ponemos 01 y después 11 solo cambiaría en el paso de un estado a otro la variable "a", teniendo b el mismo estado 1 en los dos casos.

Recuerda esta norma siempre al construir la tabla de simplificación por Karnaugh.

¿Qué representa cada cuadrado de la tabla o mapa de Karnaugh?

Una variable lógica o digital puede tener un valor de 0 o de 1.

Dos variables pueden tener los siguientes valores: 00, 01, 11 o 10. En la tabla de karnaugh, las variables invertidas toman el valor 0 y las no invertidas el valor 1.

Seguimos con el ejemplo de la tabla para 3 variables: si tenemos la variable ab y el primer cuadrado de la primera columna con valores 00 para a y b (ver imagen de arriba).

Esto significa que en ese cuadrado, el valor que se ponga dentro de el, representará el valor de la combinación de ab = 00, es decir "a" invertida por "b" invertida (a´x b´).

La tercera columna 11 representará los valores de a x b (sin invertir ninguna de las dos.

Lógicamente el valor dentro del cuadrado a su vez representará un valor c de 0 o de 1.

Por ejemplo el primer cuadro de la primera columna 00 - primera fila 0; representará el valor de la salida para el producto de a´x b´ x c´

Y el cuadro de abajo donde c es 1 representará el valor de salida para la combinación del producto: a´x b´ x c ; donde la c está sin invertir.



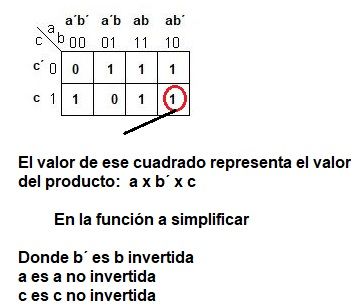
Ya tenemos nuestra tabla con los posibles valores de a, b y c.

Si te fijas, tenemos que cada cuadrado de la tabla de Karnaugh representará una sola y única combinación de las posibles combinaciones que pueden tener las variables a, b y c.

Lo mismo pasa para 2 variables, 4 variables y 5 variables.

Te dejamos un video donde se explica cómo se rellena la tabla de Karnaugh:



3º) Ahora que ya tenemos nuestra tabla o mapa de Karnaugh creada, el siguiente paso es rellenarla con los posibles valores de salida para cada producto de los valores de entrada.

Tenemos 2 posibilidades, que tengamos la tabla de la verdad o que tengamos la función lógica del circuito.

Lo normal es que nosotros hagamos la tabla de la verdad y después obtener la función lógica con la tabla de la verdad obtenida.

Si este es el caso, lo mejor es utilizar siempre la tabla de la verdad, pero puede darse el caso que tengamos una función lógica de un circuito sin nada mas.

- Si tenemos la tabla de la verdad tenemos que poner un 0 en el cuadro donde la combinación de las variables de como salida el valor 0 en la tabla de la verdad y un 1 en el cuadrado cuya combinación de variables de la salida 1 en la tabla de la verdad.

Recuerda que los productos de una función lógica son las combinaciones de las variables que dan como salida 1. Fíjate en la siguiente imagen (solo en el paso de tabla de la verdad a tabla de karnaugh).

Las combinaciones que dan como salida 1 de las variables de entrada en la tabla de la verdad, son las que en su cuadro, dentro de la tabla de karnaugh, debemos de poner un 1.



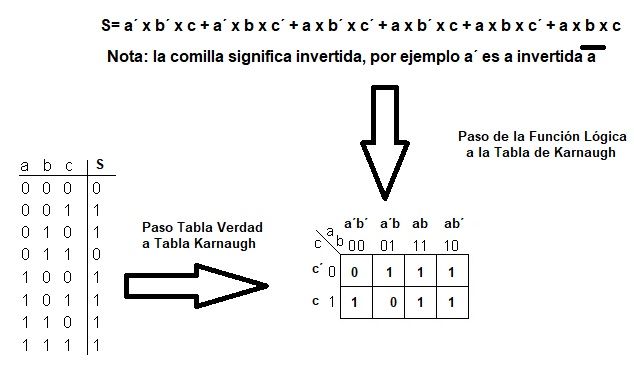
- Si tenemos la función lógica, recordar que las combinaciones de las variables de los productos de la función son las combinaciones que dan como salida un valor de 1.

Ejemplo: si tenemos esta función S = (a x b) + (a´x b)

En esta función cuando tengamos:

(a x b) o (a´ x b) la salida tendrá como resultado 1.

Recuerda el valor de la variable sin invertir (a) se supone 1 e invertida (a´) 0

Buscaremos en la tabla de karnaugh el cuadro que representa cada uno de esas multiplicaciones de variables y en esos 2 cuadros pondremos el valor de 1, en el resto el valor de 0.

Buscamos el cuadrado de a x b en la tabla de karnaugh y ponemos 1; el de a´x b y en su cuadrado también ponemos 1.

Para el resto de cuadros ponemos 0.



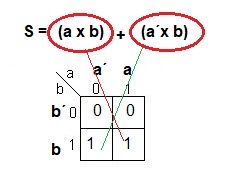
Es decir, las combinaciones de variables de los productos en la función, son las combinaciones en la tabla de karnaugh donde debemos de poner un 1 en ese cuadro.

En el ejemplo de arriba para 3 variables (ahora fíjate solo en el paso de la función lógica a la tabla de karnaugh).

El primer producto de la función lógica es a invertida, por b invertida por c sin invertir.

En el cuadrado de esa combinación de la tabla ponemos un 1 y así para todos los productos de la función lógica, que serán las combinaciones que dan un valor de salida 1.

En el resto de cuadros ponemos un 0.

Pero...¿Qué pasa si algún producto de la suma de productos de la función le falta alguna variable de entrada?

Por ejemplo imagina que tenemos S = (a x b) + (a´x b x c).

En el primer producto no tenemos la variable c.

En estos casos es un poco más compleja la solución.

Recuerda: con la tabla de la verdad esto no pasa nunca, por eso ya te dijimos, que si se puede, es mejor utilizar la tabla de la verdad.

¿Que haríamos en estos casos? Debemos obtener lo que se llama la "expresión canónica" de la función, que es una expresión con una suma de productos en la que todos los productos tengan las 3 variables (o las 2, las 4, las 5... depende las variables que tenga la función.).

¡¡¡OJO!!! la expresión canónica debe ser una función equivalente, es decir que no cambie con respecto a la función inicial.

Por el algebra de boole sabemos que una variable sin invertir mas la misma variable invertida el resultado es 1 (a + a´ = 1), y además, un producto si le multiplicamos por 1 sigue siendo el mismo producto (a x b x 1 = a x b).

Sabiendo esto, cogemos el producto de la función al que le falta una variable y lo multiplicamos por la suma de la variable que le falta sin invertir e invertida (c + c´), que ya sabemos que esta suma da un valor de 1 y no cambia el valor de la multiplicación inicial.

Veamos como quedaría en el ejemplo anterior.

Al producto que le faltaba una variable era (a x b) y le faltaba la variable c:

a x b x (c + c´) = a x b x c + a x b x c´

Esto hace que no cambie nada, la única diferencia es que ahora tenemos en lugar de un producto al que le falta una variable (a x b), dos productos con todas las variables cada uno (a x b x c + a x b x c´ ), pero que dan el mismo resultado que el producto de a x b.

El segundo término de la función inicial como no le faltaba ninguna variable queda como está.

La expresión canónica de la función sería:

S = a x b x c + a x b x c´ + + a´x b x c

OJO si tenemos varias sumas hay que comprobar si se repite alguna (si hay más de un producto igual), si pasa esto, se anularían todas las expresiones iguales y solo dejaríamos una en la suma de productos. Veamos un ejemplo:



Ahora ya tenemos nuestra función preparada para continuar con su simplificación por el diagrama de Karnaugh.

4º) Ahora llega el momento la agrupación de UNOS.

Tenemos que agrupar grupos de 1 de dos en dos, de cuatro en cuatro, de ocho en ocho etc. hasta que queden agrupados todos los UNOS de la tabla.

Tenemos que hacer grupos de 1 de 2ⁿ pudiendo ser nlos valores 0, 1, 2, 3.... que dan como resultado los valores anteriores (1, 2, 4, 8, 16, ....)

Conclusión debemos agrupar UNOS en grupos de 1, 2, 4, 8, 16....UNOS. y además, la agrupación debe ser la mayor posible de unos, y no importa que un uno o varios unos pertenezcan a varias agrupaciones siempre y cuando las agrupaciones se realicen en vertical o en horizontal (cuadrados o rectángulos) nunca en diagonal.

OJO nunca agrupar grupos de 3 o 5 unos.



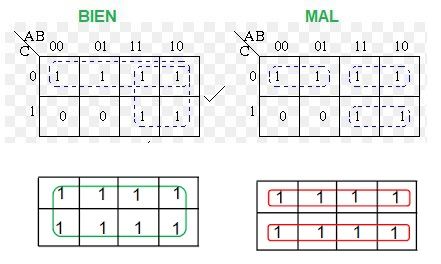
Además los grupos de los cuadros de la columna del extremo derecho de la tabla y de el extremo izquierdo se pueden agrupar.

Igualmente se pueden agrupar los grupos de unos de la fila de arriba y de abajo.

Es como si la tabla acabara por sus extremos y volviera a empezar por el otro lado.

Ver agrupaciones en la imagen de más abajo.

Veamos algunos ejemplos de agrupaciones de 1:



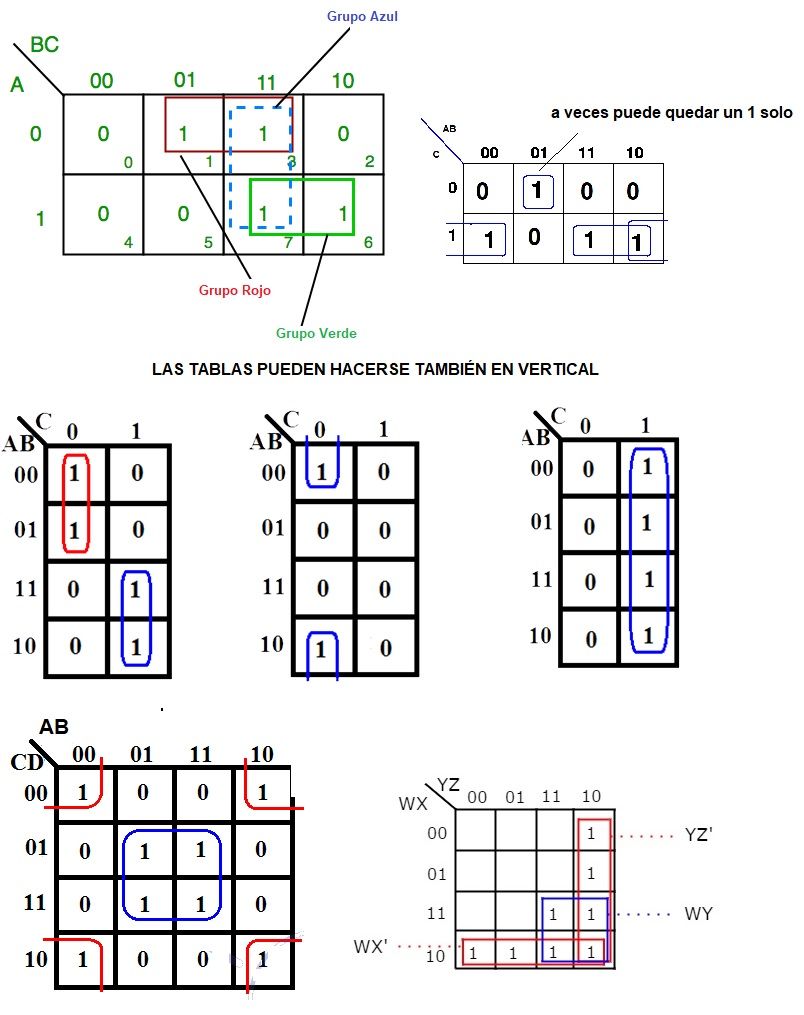
5º) Con los Grupos Obtenemos la nueva función simplificada.

Cada grupo de unos nos dará un término (un producto de la suma de productos) de la nueva función simplificada.

Estos productos se suman y obtenemos la nueva función simplificada.

Para obtener el término de la función:

Elegimos un grupo de unos y comprobamos si dentro de ese grupo, alguna variable cambia de valor, pasa de 0 a 1 (o de invertida a sin invertir).

En ese caso, esa variable (o variables) se eliminan del producto que nos daría ese grupo de unos.

Las otras que no cambian de valor multiplicadas, serán uno de los producto de la suma final de productos de la función simplificada.

OJO multiplicadas con o sin invertir, según como estén en el grupo.

Eso mismo lo hacemos en cada grupo de unos que tengamos y obtendremos tantos productos como agrupaciones de unos hayamos hecho en la tabla.

Sumamos todos los productos obtenidos y ya tenemos nuestra función simplificada.

Lo mejor es verlo sobre un ejemplo. En el ejemplo anterior:



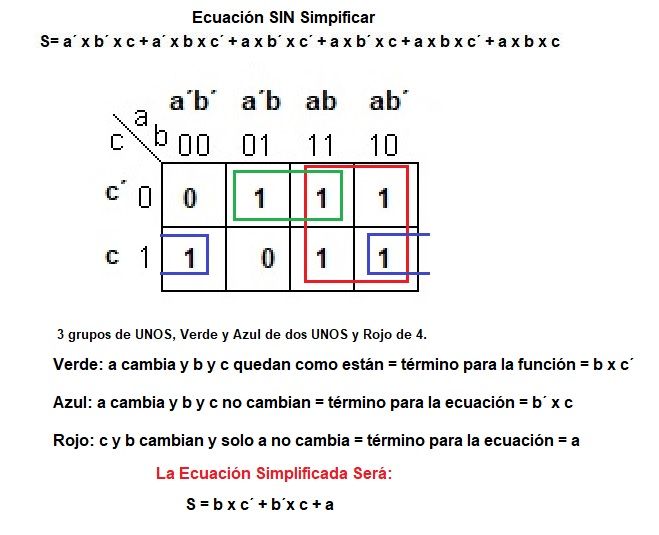
¿Por qué eliminamos las variables que cambian?

Una variable cuando se multiplica por ella y por su invertida es como si no hubiera variable, ya que el resultado sería 1.

Por este motivo es por lo que cuando tenemos una variable que cambia de valor dentro de un grupo de 1, a la hora de obtener el producto de ese grupo, simplemente la eliminamos.

Si no la elimináramos, nos quedaría esa variable en la multiplicación dos veces, una invertida y otra no invertida, algo que no debe ocurrir porque es lo mismo que 1 y lo que queremos es simplificar la función.

Mira este otro ejemplo y la gran simplificación que hacemos:



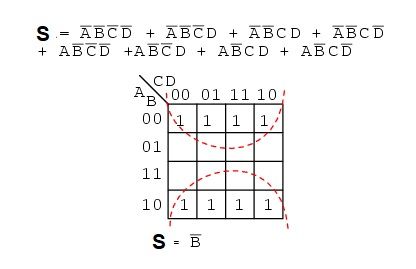
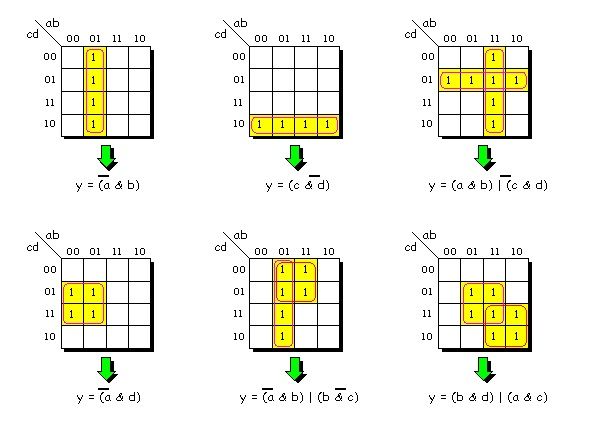
Y aquí tienes otros ejemplos. En este caso se pone un & para expresar la multiplicación y el símbolo | para la suma en la función.



VIDEO EXPLICACIÓN



Ahora que ya tenemos nuestra función simplificada, podríamos hacer el circuito lógico mediante puertas lógicas y con ese circuito de puertas construirlo o montarlo mediante circuitos integrados. Pero eso lo dejamos para explicarlo en otra ocasión.

Si quieres aprender electrónica digital de forma fácil para todos, te recomendamos el siguiente libro:



Y si lo quieres aprender electrónica analógica de forma fácil para todos, te recomendamos el siguiente libro que contiene los conceptos básicos de electrónica explicados de forma sencilla y amena:



¿Te ha gustado la web Karnaugh? Pulsa en Me gusta. Gracias por Compartir



© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.