CIRCUITOS DE CORRIENTE ALTERNA
En la parte de abajo de la página tienes un enlace a ejercicios resueltos en corriente alterna, para que una vez estudiados puedes ver como se resuelven este tipo de ejercicios.
Como ya estudiamos en la corriente alterna y continua, la corriente alterna (c.a) la producen los alternadores
Los receptores eléctricos en corriente alterna, motores, lámparas, etc., cuando se conectan en un circuito pueden tener 3 resistencias diferentes.
Antes de seguir te recomendamos el siguiente libro para aprender los principios básico de la electricidad y el cálculo de circuitos eléctricos, tanto de corriente contínua como de alterna: Libro Circuitos Eléctricos
Y Ahora también puedes hacer el curso en UDEMY para aprender a resolver circuitos de corriente contínua y si entras desde este enlace tendrás un descuento del 35% sobre el precio del curso:
https://www.udemy.com/course/circuitos-electricos-en-corriente-continua/?couponCode=9E773C2AD5BFB19CE634
Si tenemos un conductor, sería prácticamente el único receptor resistivo puro y en este caso si calculamos la resistencia que ofrece al paso de la corriente por ser un conductor sería:

Donde L es la longitud del cable en metros, S la sección del cable en milímetros cuadrados y p es la resistividad del conductor o cable, un valor que nos da el fabricante del cable.
Nota: un cable no es un receptor, pero bueno.
Los hornos eléctricos, los radiadores y las lámparas incandescentes se consideran receptores resistivos puros (R) y se calculan igual que en corriente continua.
Ejemplo: Calcula la resistencia de un cable de alumino e aluminio de 2 Km de longitud y 1 mm2 de sección. Resistividad del Alumnio = 0,028 Ωmm2/m
R = 0,028 x ( 2.000m/1) = 56 Ω (ohmios)
- Una Resistencia XL = resistencia o reactancia inductiva que solo tienen las bobinas (espiras) por su inductancia.
Su valor es XL = L x w
L se mide en Henrios (H) y es el coeficiente de autoinducción de la bobina, también llamado Inductancia.
w = 2 x π x f; donde f es la frecuencia y se mide en Hertzios (Hz).
XL por ser una resistencia se mide en Ohmios (Ω)
Una reactancia de un tubo fluorescente se puede considerar un receptor inductivo puro (L).
Ejemplo: Un inductor o bobina de 0.1 H se conecta a una fuente de CA con una frecuencia de 60 Hz. Calcula la reactancia inductiva.
Ahora te toca a ti:
Ejercicio 1: Un inductor o bobina de 0.3 Henrios se conecta a una fuente de CA con
una frecuencia de 50 Hz.
Calcula la reactancia inductiva. solución: 94,24Ω
- Una Resistencia XC = resistencia o reactancia capacitiva que solo tienen los condensadores.
Su valor es Xc = 1/(C x w)
C es la capacidad del condensador y se mide en Faradios.
Xc por ser una resistencias se mide en Ohmios (Ω)
Los condensadores y sensores capacitivos se consideran receptores capacitivos puros (C).
Ejemplo: Un condensador tiene una capacidad de 0,00005 F y se conecta a una fuente de corriente alterna con una frecuencia de 60 Hz.
Calcula la reactancia capacitiva.
Xc = 1/(C x w) = 1 / ( 0,00005 x 2 x 3,1416 x 60) = 53,052 Ω
Ahora te toca a ti:
Ejercicio 2: Un condensador tiene una capacidad de 0,0008 F y se conecta a una fuente de corriente alterna con una frecuencia de 50 Hz.
Calcula la reactancia capacitiva. solución: 3,97 Ω
En la vida real hay muy pocos receptores de corriente alterna que se pueda considerar que solo tengan “R”, solo “L” o solo C ya que por ejemplo, la bobina de un motor será un receptor inductivo, pero al ser un conductor también tendrá una resistencia, y por lo tanto, también tendrá un componente resistivo, por lo que realmente será un receptor RL.
Los motores, los transformadores y los electroimanes suelen considerarse RL, receptores inductivos, pero no puros, ya que tienen también R.
Incluso algunos motores también tienen un condensador para su arranque, por lo que serán receptores RLC.
Conclusión: Los receptores en alterna pueden tener resistencia resistiva (R), inductiva (XL), capacitiva (XC) o una mezcla de 2 o 3 de ellas.
Después de lo visto.....
La resistencia total real de un receptor en ca se llama “Impedancia” (Z).
Lógicamente si un receptor solo tiene R entonces Z=R, Si solo tiene XL entonces Z=XL, y si solo tiene XC entonces Z=Xc
Como la mayoría tiene 2 o 3 de las resistencias anteriores, vamos a ver la fórmula para su cálculo, aunque luego veremos de dónde sale el triángulo de impedancias y su demostración:
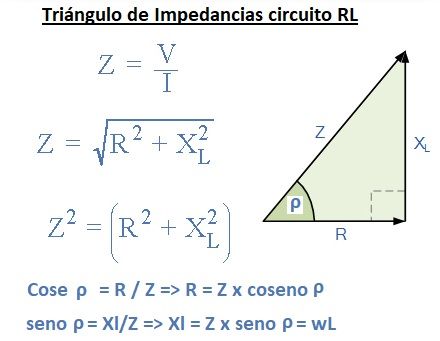
Ejemplo: Un receptor tiene una resistencia resistiva de 30 Ω y un inductor de 0.1 H. Si la frecuencia de la fuente es de 50 Hz, calcula:
1)La reactancia inductiva.
2) La impedancia total del circuito.

Ya conocemos la resistencia total, mejor dicho, la impedancia de un receptor en c.a o de varios.
Ahora vamos a conectarlo a una fuente de tensión en alterna, un alternador o enchufe por ejemplo, y entonces el circuito se cerrará y comenzará a circular corriente eléctrica en alterna.
Pero antes de ver como son y como se resuelven los circuitos en corriente alterna, es necesario tener claro los conceptos de la corriente alterna, los fasores o vectores de la Tensión e Intensidad y el desfase entre ellos.
Si no los tienes te recomendamos que antes estudies la siguiente web: Corriente Alterna y Continua. O veas el siguiente video: La Corriente Alterna
Recordamos que el valor más representativo de una magnitud eléctrica senoidal alterna va a ser su valor eficaz (V) y su desfase, recordamos que
Vmax = Vo = Veficaz x √2.
Si nos diesen la ecuación o función de una onda de corriente alterna, como en la ecuación de una onda alterna tenemos el valor máximo, si queremos calcular el valor eficaz sería:
v = Vo sen wt
Veficaz = Vo / √2.
Los valores eficaces de la tensión y de la intensidad son los más utilizados, y son los que nos miden los aparatos de medida como el polímetro.
Exactamente el valor eficaz de la intensidad es I = Io / √2 (en monofásica, en trifásica es dividido entre raiz de 3)
La tensión eficaz, según la ley de ohm, es V = I/Z ; intensidad eficaz partido por la impedancia (luego hablaremos de ella)
Ahora si, veamos nuestro circuito.
La corriente total es una mezcla de la corriente que necesita cada una de las diferentes resistencias que tenga el receptor.
-La parte R absorberá una intensidad que llamaremos Intensidad activa (Ia o IR ) y estará en fase con V
-La parte XL absorberá una intensidad que llamaremos intensidad reactiva inductiva (IL) y desfasada - 90º respecto a la V
-La parte Xc absorberá una intensidad que llamaremos intensidad reactiva capacitiva (Ic) desfasada + 90º respecto a la V
Si las representamos por separado mediante sus fasores serían:

Para un receptor que tenga RLC habrá que sumar las 3 intensidades vectorialmente para obtener la intensidad total real que absorbe y pasa por el receptor.

Como puedes ver, el que el receptor tenga una mezcla de 2 o 3 de las resistencias es por lo que se produce el desfase de la intensidad y la tensión y estará entro 0º y 90º o -90º, dependiendo de la cantidad de R, XL y XC que tenga el receptor.
Por ejemplo puede tener ángulo de 10º, 35º, etc.
Como la intensidad es provocada por cada una de las resistencias, igual que obtenemos el triángulo de intensidades, tendremos también un triángulo de impedancias (R, Xl y Xc)

Ahora sí, ya podemos empezar a calcular magnitudes de corriente alterna.
Tanto las intensidades, como las impedancias forman un triángulo rectángulo, que precisamente será el que utilizaremos para hacer los cálculos.

Ejemplo: Calcula la intensidad total, también llamada aparente, y el coseno de fi de un motor que tiene una intensidad inductiva de 1A y una intensidad resistiva de 3 A

Ya tenemos el triángulo de intensidades y de impedancias, pero…
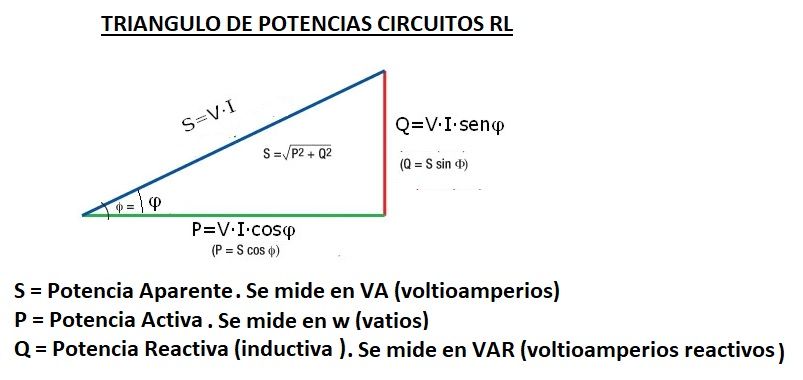
Q será el resultado de restar QL - QC
S = V x I; (Tensión e Intensidad Eficaces) y según el triángulo:
P = V x I x cos φ (fi) = S x cos φ (fi)
Q = V x I x seno φ (fi) = S x seno φ (fi)
Importante: de las 3 potencias solo se transforma en trabajo útil la potencia activa (Pa) y es la que viene en la placa de características del aparato en w o Kw.
La S o aparente es la que consume en total el receptor, y la Q será las pérdidas de potencia que tenga.
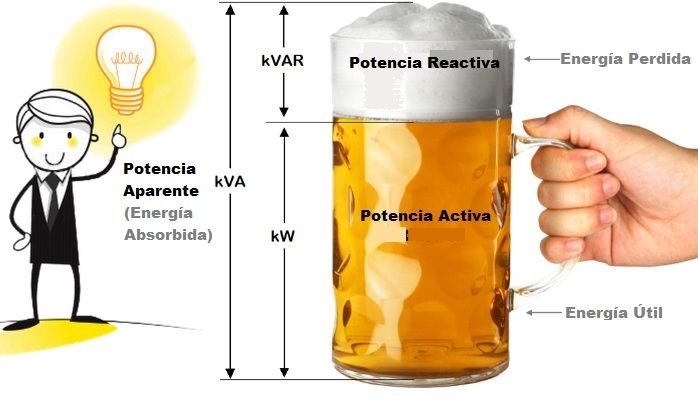
Para calcular las potencias se hace de igual forma que las impedancias o intensidades, mediante resolución de los triángulos.
Ejemplo: Tenemos un circuito con Veficaz=220V, Ieficaz= 5A y ángulo θ=30º. Calcula la potencia Aparente, Activa y Reactiva.
Nota: a veces el ángulo φ, se pone θ
S = V x I = 220 x 5 = 1100VA
P = V x I x cos (θ) = 220 x 5 x cose 30º = 1.110 x 0,866 = 954,4 w
Q = V x I x seno (θ) ) 220 x 5 x seno 30º = 1.100 x 0,5 = 550VAR
Ahora imagina que de alguna forma bajamos el ángulo fi a 10º ¿En qué caso tendrá menos pérdidas?
Q = V x I x seno (θ) = 220 x 5 x seno 10º = 1.100 x 0,17 = 191 VAR
Mucho menos pérdidas si bajamos el ángulo y el vector S se acerca a la Pa.
Recuerda Si fi = 0º ==> cos fi = 1
Si una instalación o un receptor tuviera un coseno de fi muy bajo, por ejemplo 0,7 o menos, entonces habría que mejorarlo mediante condensadores.
Recuerda que el coseno fi también se puede calcular con las potencias, de hecho a este valor, al del coseno de fi se le llama factor de potencia.
Factor de Potencia = coseno φ = Pa / S
Ejemplo: En un circuito de c.a. un vatímetro marca 1Kw, el amperímetro marca 6A y el voltímetro marca 230V. Calcula el factor de potencia, fdp o coseno de fi
coseno φ = Pa / S = 1.000w / (230V x 6A) = 0,72
Ahora veamos como se comportan los circuitos en corriente alterna en función del receptor que se conecte.
CIRCUITOS R
Solo están compuesto con elementos resistivos puros.
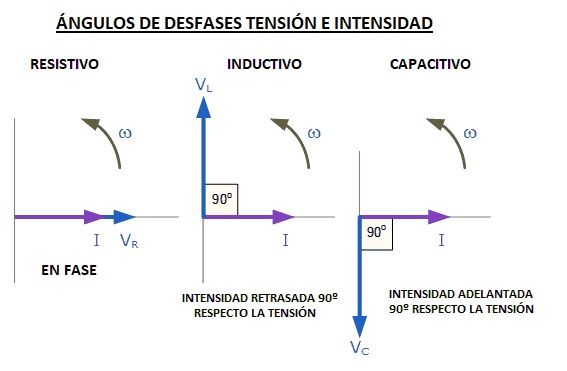
En este caso la V y la I (tensión e intensidad) están en fase, o lo que es lo mismo, las ondas empiezan y acaban a la vez en el tiempo.
Por estar en fase se tratan igual que en corriente continua.
Esto en c.a. solo pasa en circuitos puramente resistivos (solo resistencias puras).
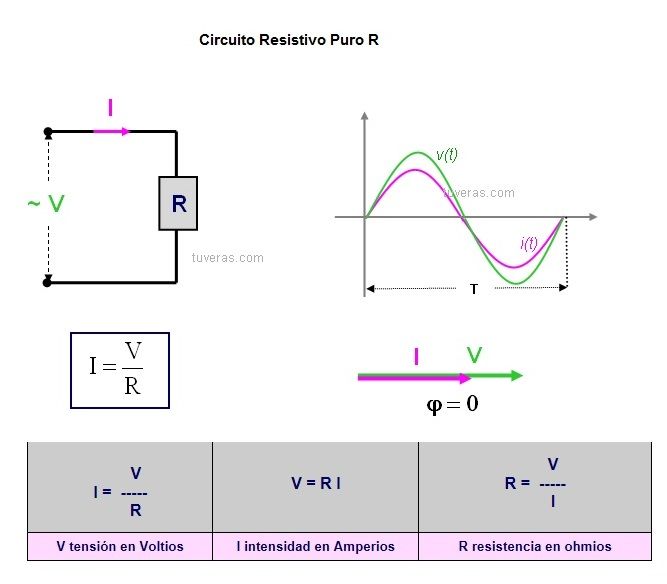
Las tensiones e intensidades instantáneas están en fase y serán:
v = Vo x seno wt
i = Io x sen wt
En receptores resistivos puros la impedancia es R, ya que no hay más tipos de resistencias.
Si te fijas lo único que hacemos es aplicar la Ley de Ohm. V = I x R.
La potencia será P = V x I. ( el cos 0º = 1), solo hay potencia activa y se llama igualmente P.
Recuerda que en este caso el ángulo de desfase es 0 grados, ya que están en fase las dos ondas.
CIRCUITOS L
Son los circuitos que solo tienen componente inductivo (bobinas puras). En este caso la V y la I están desfasadas 90º.
La intensidad esta retrasada 90º respecto a la tensión o la tensión está adelantada 90º respecto a la intensidad.
En estos circuitos en lugar de R tenemos Xl, impedancia inductiva.
La Xl es algo así como la resistencia de la parte inductiva.
Para calcularla es importante un valor llamado inductancia (L) que solo poseen las bobinas puras.
L será la inductancia y se mide en henrios, al multiplicarla por w (frecuencia angular) nos dará la impedancia inductiva.
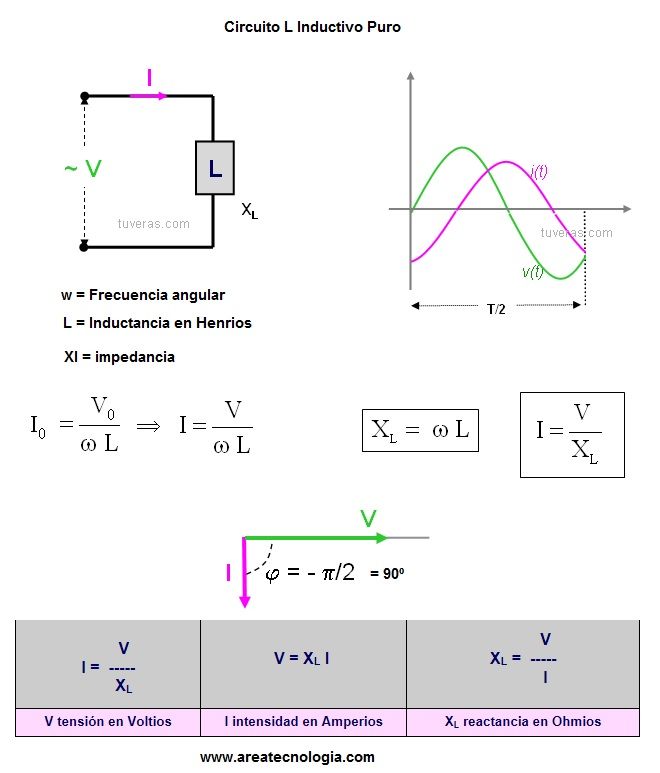
Si consideramos la XL como la resistencia (resistencia inductiva), aplicando la Ley de Ohm generalizada, los valores eficaces son:
I = V/wL e I V/Xl siendo Xl = w x L.
El valor de la tensión en cualquier momento (instantánea) sería:
v = Vo x sen wt ; donde Vo es el valor máximo de la tensión, w frecuencia angular y t el tiempo.
Para la intensidad instantánea recuerda que la I está retrasada 90º respecto a la tensión.
Si wt es el ángulo para la tensión, como la intensidad está retrasada 90º respecto a la tensión, tenemos que la intensidad instantánea será:
i = Io x seno (wt - 90º)
CIRCUITOS C
Este tipo de circuitos son los que solo tienen componentes capacitivos (condensadores puros).
En este caso la V y la I están desfasadas 90º negativos (la V está retrasada en lugar de adelantada con respecto a la I).
La Xc será la impedancia capacitiva, algo parecido a la resistencia de la parte capacitiva.
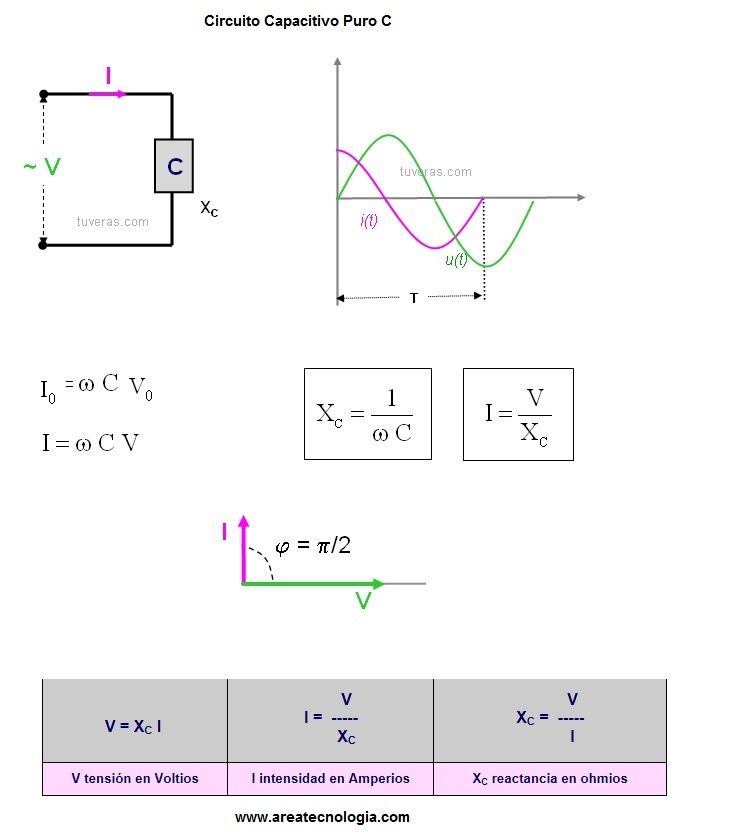
Los valores eficaces, considerando la resistencia Xc (resistencia capacitiva) y aplicando la ley de ohm generalizada son:
I = V/Xc e I = V/Xc; siendo Xc = 1/wC.
El valor de la tensión en cualquier momento sería:
v = Vo x sen wt ; donde Vo es el valor inicial de la tensión, w frecuencia angular y t el tiempo.
Igualmente la intensidad:
i = Io x seno (wt + 90º), recuerda que la I está adelantada 90º.
Si quieres saber todo sobre los condensadores te recomendamos este enlace: Condensador.
Ahora que ya sabemos como se resuelven los circuitos de corriente alterna con receptores puros, veamos como se resuelven cuando son una mezcla de varios puros.
En este caso tenemos varias posibilidades, RL, RC y RLC.
Recuerda los ángulos de desfase en cada caso.
Es mejor para los circuitos en serie recordar los ángulos de desfase tomando como referencia en 0º a la intensidad.
En ese caso mira como quedarían:
CIRCUITO RL EN SERIE
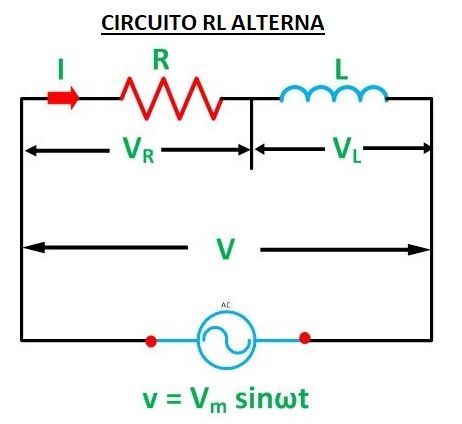
Por ser un circuito en serie, la intensidad por los 2 receptores serán las mismas, y las tensiones serán la suma de las 2 tensiones, pero OJO, suma vectorial porque recuerda que están desfasadas-.
Si consideramos que la intensidad está en ángulo 0, la tensión de la resistencia estará en fase, pero la de la bobina estará adelantada 90º respecto a la intensidad del circuito y por lo tanto 90º adelantada respecto a la tensión de la resistencia también.
Podríamos dibujar las 3 tensiones en lo que se llama el triángulo de tensiones:
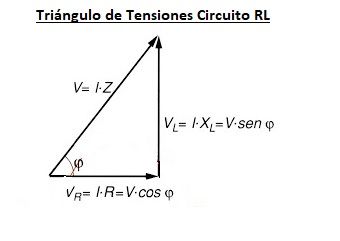
De este triángulo podemos deducir muchas fórmulas, solo tenemos que aplicar trigonometria.
Si ahora dividimos todos los vectores del triángulo entre la intensidad, nos queda un triángulo semejante pero más pequeño, que será el llamado triángulo de impedancias.

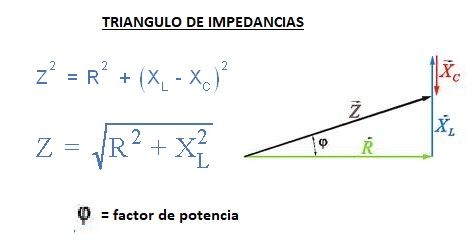
Por trigonometría podemos deducir varias fórmulas de este triángulo, como puedes ver en la imagen.
Potencias en Corriente Alterna
¿Qué pasaría si en el triángulo de tensiones multiplicamos todas las tensiones por la intensidad?
Pues que tendríamos el llamado triángulo de potencias, un triángulo semejante al de tensiones pero con valores mayores de los vectores.

De este triángulo, igual que con los demás, podemos deducir varias fórmulas por trigonometría.
Pero lo que está claro es que en corriente alterna las potencias son 3 diferentes.
Potencia Activa Pa = V x I cose ρ ; esta es la única que da trabajo útil, la realmente transformada.
Se mide en Vatios (w). Es la tensión eficaz, por la intensidad eficaz, por el coseno del ángulo que forman.
Potencia Reactiva S = V x I seno ρ ; esta es como si fuera una potencia perdida, cuanto menor sea mejor.
Se mide en voltio amperios reactivos (VAR)
Potencia Aparente Q = V x I ; se mide en voltio amperios (VA).
En cuanto a las potencias en alterna no estudiaremos más porque se nos haría el tema excesivamente largo.
Si quieres ampliar vete a este enlace: Potencia Eléctrica, donde se explican más detalladamente todas las potencias incluidas las de alterna.
Veamos un ejercicio sencillo y muy típico de un motor de corriente alterna, circuito RL:

En la parte de abajo tienes un enlace a una página con muchos más ejercicios resueltos de corriente alterna.
El circuito RL tiene un componente resistivo y otro inductivo (R y L).
Podemos trabajar con números complejos para resolver estos circuitos, o con los triángulos que hemos visto hasta ahora por trigonometría.
Veamos cómo sería si la impedancia la tratáramos como un número complejo.
Como en el componente resistivo la i y la v están en fase, el ángulo de desfase depende de la cantidad de componente inductivo que tenga.
Z = R + Xlj , como Xl= w x L (frecuencia angular por inductancia) podemos decir también Z = R + (w x L) j
¿No sabes lo que es un número complejo?
No te preocupes, es muy fácil aprender a trabajar con ellos, y para estos circuitos nos facilita mucho el trabajo.
Un número complejo (Z) en los Circuitos Electricos, lo utilizamos para representar con el llamado triángulo de impedancias:
Z = R + Xj; fíjate que a la parte X del número complejo (representada en el triángulo como un cateto) se le pone un j para representar el número complejo.
Ya está, así de fácil es un número complejo, lo que realmente representa un número complejo es un triángulo (hipotenusa y sus dos catetos).
Sigamos con nuestro circuito.
En los circuitos de corriente alterna el número complejo representa la impedancia del circuito (hipotenusa, Z), la resistencia de la parte resistiva pura (cateto R) y la diferencia (resta vectorial) entre la impedancia inductiva y la capacitiva (X = Xl - Xc), esta última con la letra j.
A la X se le llama Reactancia.
En los circuitos RL no tenemos Xc, por lo que X sería igual a Xl, si tuviéramos Xc (parte capacitiva), X sería (Xl-Xc) una resta de los dos vectores, como en nuestro caso no tenemos Xc, entonces X = Xl.
Según este triángulo podemos convertir el número complejo en número natural con la siguiente fórmula (por Pitágoras):
Z2 = R2 + Xl2Podríamos despejar Z para calcularla.
La intensidad sería I = V / Z, que en instantánea quedaría:
i = (Vo x seno wt) / (R + wLj) en complejo. Podemos convertirlo en eficaz sustituyendo la Z por la raíz cuadrada de (R + wL).
Los valores eficaces serían V = I /Z o I = V/Z.
CIRCUITO RC
Este es igual solo que ahora tenemos Xc en lugar de Xl. Recuerda que Xc = 1/wC.
La intensidad será la misma en el circuito por estar los dos componentes en serie, pero la tensión será la suma.
La diferencia con el anterior es que la tensión del condensador estará retrasada 90º con respecto a la intensidad, no adelantada como con la bobina.
Tendremos los mismos triángulo, pero boca abajo.
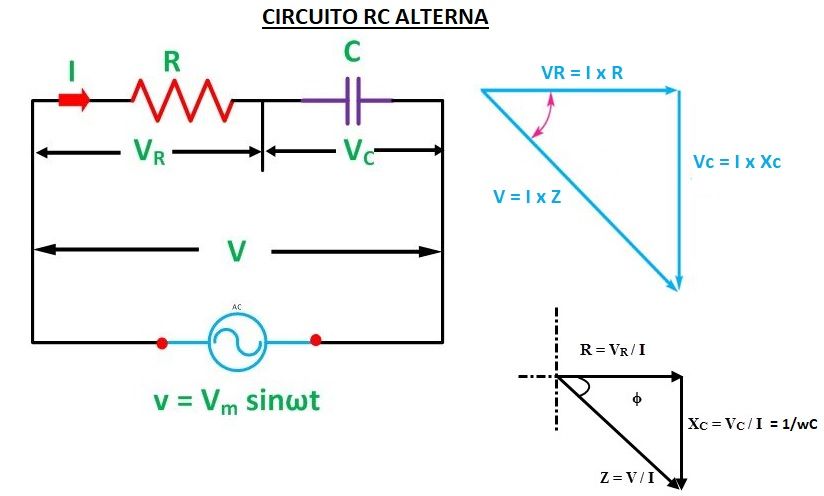
Además, si trabajamos con números complejos tenemos: Xc = 1/(wCj) y por lo tanto Z = R + 1/(wCj) en numero complejo.
Pero si hacemos el triangulo de impedancias en este caso la Z en número natural sería:
Z2 = R2 + (1/(wC))2
Ves que es igual pero sustituyendo Xl por Xc que es 1/wC, en lugar de Xl que es wL.
Ahora vamos analizar los circuito RLC que son los más interesantes:
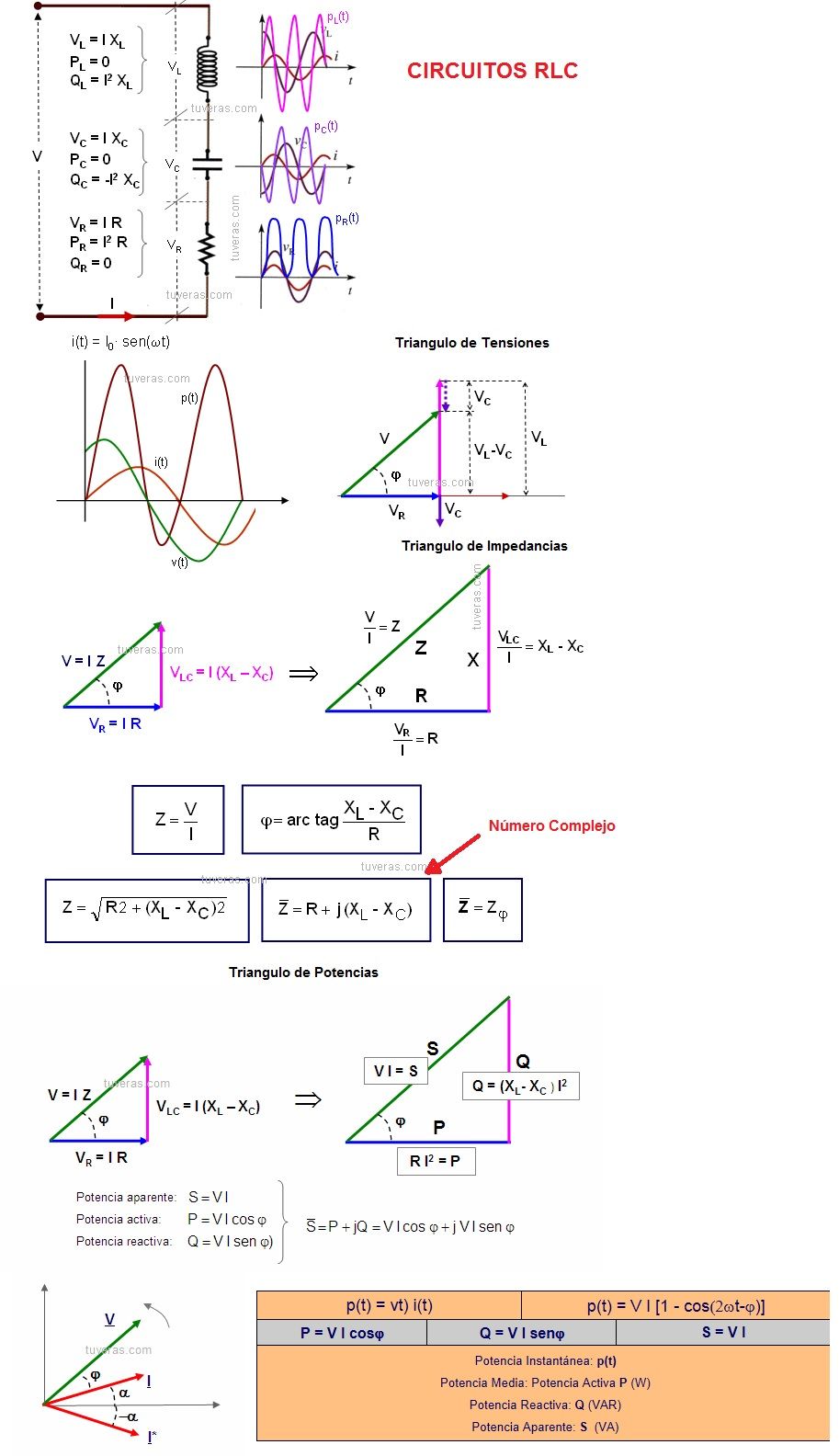
CIRCUITOS RLC
Son los circuitos más reales.
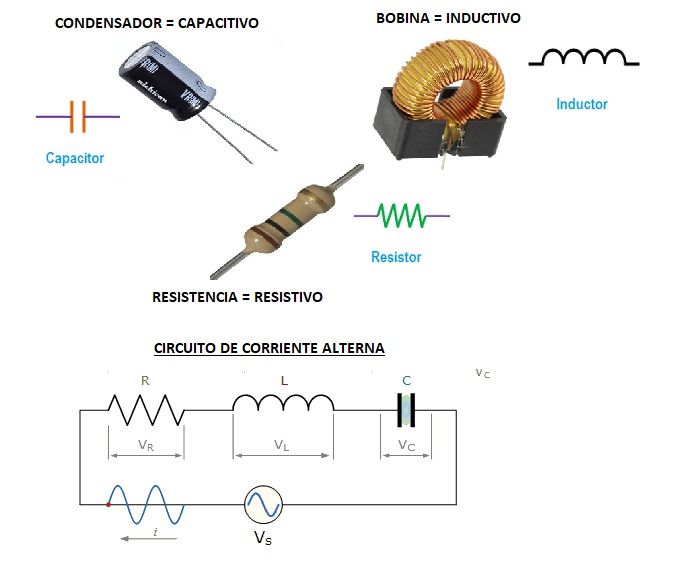
Fíjate que si te acostumbras hacer todo con los triángulos de impedancias, de tensiones y de potencias es mucho más fácil.
Para resolver los circuitos de corriente alterna en paralelo, basta con aplicar a los circuitos la ley de ohm generalizada y las leyes de kirchhoff.
Además recuerda que en paralelo la tensión aplicada a cada elemento del circuito (R, L o C) es la misma y la intensidad por cada uno de ellos es distinta, por lo que no hay triángulo de tensiones, hay triángulo de intensidades.
Todo esto lo veremos en esta otra web para no hacerlo muy extenso: Circuitos RLC en Paralelo.
Ahora deberías ir a ver los ejercicios resueltos de c.a.: Ejercicios Alterna
También te puede interesar conocer y aprender los Sistemas Trifásicos, ya que los aqui estudiados son monofásicos.
Por último te recomendamos si quieres aprender a resolver todo tipo de circuitos eléctricos de forma fácil, el siguiente libro: Libro Circuitos Eléctricos
Y Ahora también puedes hacer el curso en UDEMY para aprender a resolver circuitos de corriente contínua y si entras desde este enlace tendrás un descuento del 35% sobre el precio del curso:
https://www.udemy.com/course/circuitos-electricos-en-corriente-continua/?couponCode=9E773C2AD5BFB19CE634
OJO la promoción caduca
Si te ha gustado haz click en Compartir, Gracias:
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
Como ya estudiamos en la corriente alterna y continua, la corriente alterna (c.a) la producen los alternadores
Los receptores eléctricos en corriente alterna, motores, lámparas, etc., cuando se conectan en un circuito pueden tener 3 resistencias diferentes.
Antes de seguir te recomendamos el siguiente libro para aprender los principios básico de la electricidad y el cálculo de circuitos eléctricos, tanto de corriente contínua como de alterna: Libro Circuitos Eléctricos
Y Ahora también puedes hacer el curso en UDEMY para aprender a resolver circuitos de corriente contínua y si entras desde este enlace tendrás un descuento del 35% sobre el precio del curso:
https://www.udemy.com/course/circuitos-electricos-en-corriente-continua/?couponCode=9E773C2AD5BFB19CE634
Las 3 Resistencias de los Receptores y Circuitos en Alterna
- Receptores R = Resistivos puros: Solo tienen una resistencia por la propia resistencia del conductor llamada resistencia óhmica “R” y que se mide en ohmios (Ω), como cualquier resistencia.Si tenemos un conductor, sería prácticamente el único receptor resistivo puro y en este caso si calculamos la resistencia que ofrece al paso de la corriente por ser un conductor sería:

Donde L es la longitud del cable en metros, S la sección del cable en milímetros cuadrados y p es la resistividad del conductor o cable, un valor que nos da el fabricante del cable.
Nota: un cable no es un receptor, pero bueno.
Los hornos eléctricos, los radiadores y las lámparas incandescentes se consideran receptores resistivos puros (R) y se calculan igual que en corriente continua.
Ejemplo: Calcula la resistencia de un cable de alumino e aluminio de 2 Km de longitud y 1 mm2 de sección. Resistividad del Alumnio = 0,028 Ωmm2/m
R = 0,028 x ( 2.000m/1) = 56 Ω (ohmios)
- Una Resistencia XL = resistencia o reactancia inductiva que solo tienen las bobinas (espiras) por su inductancia.
Su valor es XL = L x w
L se mide en Henrios (H) y es el coeficiente de autoinducción de la bobina, también llamado Inductancia.
w = 2 x π x f; donde f es la frecuencia y se mide en Hertzios (Hz).
XL por ser una resistencia se mide en Ohmios (Ω)
Una reactancia de un tubo fluorescente se puede considerar un receptor inductivo puro (L).
Ejemplo: Un inductor o bobina de 0.1 H se conecta a una fuente de CA con una frecuencia de 60 Hz. Calcula la reactancia inductiva.
Ahora te toca a ti:
Ejercicio 1: Un inductor o bobina de 0.3 Henrios se conecta a una fuente de CA con
una frecuencia de 50 Hz.
Calcula la reactancia inductiva. solución: 94,24Ω
- Una Resistencia XC = resistencia o reactancia capacitiva que solo tienen los condensadores.
Su valor es Xc = 1/(C x w)
C es la capacidad del condensador y se mide en Faradios.
Xc por ser una resistencias se mide en Ohmios (Ω)
Los condensadores y sensores capacitivos se consideran receptores capacitivos puros (C).
Ejemplo: Un condensador tiene una capacidad de 0,00005 F y se conecta a una fuente de corriente alterna con una frecuencia de 60 Hz.
Calcula la reactancia capacitiva.
Xc = 1/(C x w) = 1 / ( 0,00005 x 2 x 3,1416 x 60) = 53,052 Ω
Ahora te toca a ti:
Ejercicio 2: Un condensador tiene una capacidad de 0,0008 F y se conecta a una fuente de corriente alterna con una frecuencia de 50 Hz.
Calcula la reactancia capacitiva. solución: 3,97 Ω
En la vida real hay muy pocos receptores de corriente alterna que se pueda considerar que solo tengan “R”, solo “L” o solo C ya que por ejemplo, la bobina de un motor será un receptor inductivo, pero al ser un conductor también tendrá una resistencia, y por lo tanto, también tendrá un componente resistivo, por lo que realmente será un receptor RL.
Los motores, los transformadores y los electroimanes suelen considerarse RL, receptores inductivos, pero no puros, ya que tienen también R.
Incluso algunos motores también tienen un condensador para su arranque, por lo que serán receptores RLC.
Conclusión: Los receptores en alterna pueden tener resistencia resistiva (R), inductiva (XL), capacitiva (XC) o una mezcla de 2 o 3 de ellas.
Después de lo visto.....
¿Qué Resistencia Tiene un Receptor en Corriente Alterna?
Pues será la suma de las resistencias que tenga de las 3 vistas anteriormente, pero OJO, la “suma vectorial de las 2 o 3 resistencias que tenga”La resistencia total real de un receptor en ca se llama “Impedancia” (Z).
Lógicamente si un receptor solo tiene R entonces Z=R, Si solo tiene XL entonces Z=XL, y si solo tiene XC entonces Z=Xc
Como la mayoría tiene 2 o 3 de las resistencias anteriores, vamos a ver la fórmula para su cálculo, aunque luego veremos de dónde sale el triángulo de impedancias y su demostración:

Ejemplo: Un receptor tiene una resistencia resistiva de 30 Ω y un inductor de 0.1 H. Si la frecuencia de la fuente es de 50 Hz, calcula:
1)La reactancia inductiva.
2) La impedancia total del circuito.

Ya conocemos la resistencia total, mejor dicho, la impedancia de un receptor en c.a o de varios.
Ahora vamos a conectarlo a una fuente de tensión en alterna, un alternador o enchufe por ejemplo, y entonces el circuito se cerrará y comenzará a circular corriente eléctrica en alterna.
Pero antes de ver como son y como se resuelven los circuitos en corriente alterna, es necesario tener claro los conceptos de la corriente alterna, los fasores o vectores de la Tensión e Intensidad y el desfase entre ellos.
Si no los tienes te recomendamos que antes estudies la siguiente web: Corriente Alterna y Continua. O veas el siguiente video: La Corriente Alterna
Recordamos que el valor más representativo de una magnitud eléctrica senoidal alterna va a ser su valor eficaz (V) y su desfase, recordamos que
Vmax = Vo = Veficaz x √2.
Si nos diesen la ecuación o función de una onda de corriente alterna, como en la ecuación de una onda alterna tenemos el valor máximo, si queremos calcular el valor eficaz sería:
v = Vo sen wt
Veficaz = Vo / √2.
Los valores eficaces de la tensión y de la intensidad son los más utilizados, y son los que nos miden los aparatos de medida como el polímetro.
Exactamente el valor eficaz de la intensidad es I = Io / √2 (en monofásica, en trifásica es dividido entre raiz de 3)
La tensión eficaz, según la ley de ohm, es V = I/Z ; intensidad eficaz partido por la impedancia (luego hablaremos de ella)
Ahora si, veamos nuestro circuito.
La Intensidad en Alterna
Cuando conectamos el receptor, que tiene una mezcla de las 3 resistencias diferentes vistas anteriormente, el receptor pedirá para su funcionamiento (absorberá) una corriente en alterna para vencer esas 3 resistencias.La corriente total es una mezcla de la corriente que necesita cada una de las diferentes resistencias que tenga el receptor.
-La parte R absorberá una intensidad que llamaremos Intensidad activa (Ia o IR ) y estará en fase con V
-La parte XL absorberá una intensidad que llamaremos intensidad reactiva inductiva (IL) y desfasada - 90º respecto a la V
-La parte Xc absorberá una intensidad que llamaremos intensidad reactiva capacitiva (Ic) desfasada + 90º respecto a la V
Si las representamos por separado mediante sus fasores serían:

Para un receptor que tenga RLC habrá que sumar las 3 intensidades vectorialmente para obtener la intensidad total real que absorbe y pasa por el receptor.

Como puedes ver, el que el receptor tenga una mezcla de 2 o 3 de las resistencias es por lo que se produce el desfase de la intensidad y la tensión y estará entro 0º y 90º o -90º, dependiendo de la cantidad de R, XL y XC que tenga el receptor.
Por ejemplo puede tener ángulo de 10º, 35º, etc.
Como la intensidad es provocada por cada una de las resistencias, igual que obtenemos el triángulo de intensidades, tendremos también un triángulo de impedancias (R, Xl y Xc)

Ahora sí, ya podemos empezar a calcular magnitudes de corriente alterna.
Tanto las intensidades, como las impedancias forman un triángulo rectángulo, que precisamente será el que utilizaremos para hacer los cálculos.

Ejemplo: Calcula la intensidad total, también llamada aparente, y el coseno de fi de un motor que tiene una intensidad inductiva de 1A y una intensidad resistiva de 3 A

Ya tenemos el triángulo de intensidades y de impedancias, pero…
¿Cómo son las Potencias en Corriente Alterna?
La fórmula de la potencia en general es V x I, y en el caso de corriente alterna, como tenemos 3 intensidades, pues tendremos que un receptor en corriente alterna tiene 3 potencias diferentes:
Q será el resultado de restar QL - QC
S = V x I; (Tensión e Intensidad Eficaces) y según el triángulo:
P = V x I x cos φ (fi) = S x cos φ (fi)
Q = V x I x seno φ (fi) = S x seno φ (fi)
Importante: de las 3 potencias solo se transforma en trabajo útil la potencia activa (Pa) y es la que viene en la placa de características del aparato en w o Kw.
La S o aparente es la que consume en total el receptor, y la Q será las pérdidas de potencia que tenga.

Para calcular las potencias se hace de igual forma que las impedancias o intensidades, mediante resolución de los triángulos.
Ejemplo: Tenemos un circuito con Veficaz=220V, Ieficaz= 5A y ángulo θ=30º. Calcula la potencia Aparente, Activa y Reactiva.
Nota: a veces el ángulo φ, se pone θ
S = V x I = 220 x 5 = 1100VA
P = V x I x cos (θ) = 220 x 5 x cose 30º = 1.110 x 0,866 = 954,4 w
Q = V x I x seno (θ) ) 220 x 5 x seno 30º = 1.100 x 0,5 = 550VAR
Ahora imagina que de alguna forma bajamos el ángulo fi a 10º ¿En qué caso tendrá menos pérdidas?
Q = V x I x seno (θ) = 220 x 5 x seno 10º = 1.100 x 0,17 = 191 VAR
Mucho menos pérdidas si bajamos el ángulo y el vector S se acerca a la Pa.
¿Qué pasa si el coseno de fi es igual a 1?
Pues que toda la potencia del receptor es potencia activa, es decir no tiene pérdidas, que sería lo ideal, por eso hay que intentar que los receptores en corriente alterna tengan un coseno de fi lo más cercano a 1, por ejemplo 0,9 estaría bien.Recuerda Si fi = 0º ==> cos fi = 1
Si una instalación o un receptor tuviera un coseno de fi muy bajo, por ejemplo 0,7 o menos, entonces habría que mejorarlo mediante condensadores.
Recuerda que el coseno fi también se puede calcular con las potencias, de hecho a este valor, al del coseno de fi se le llama factor de potencia.
Factor de Potencia = coseno φ = Pa / S
Ejemplo: En un circuito de c.a. un vatímetro marca 1Kw, el amperímetro marca 6A y el voltímetro marca 230V. Calcula el factor de potencia, fdp o coseno de fi
coseno φ = Pa / S = 1.000w / (230V x 6A) = 0,72
Ahora veamos como se comportan los circuitos en corriente alterna en función del receptor que se conecte.
CIRCUITOS R
Solo están compuesto con elementos resistivos puros.
En este caso la V y la I (tensión e intensidad) están en fase, o lo que es lo mismo, las ondas empiezan y acaban a la vez en el tiempo.
Por estar en fase se tratan igual que en corriente continua.
Esto en c.a. solo pasa en circuitos puramente resistivos (solo resistencias puras).

Las tensiones e intensidades instantáneas están en fase y serán:
v = Vo x seno wt
i = Io x sen wt
En receptores resistivos puros la impedancia es R, ya que no hay más tipos de resistencias.
Si te fijas lo único que hacemos es aplicar la Ley de Ohm. V = I x R.
La potencia será P = V x I. ( el cos 0º = 1), solo hay potencia activa y se llama igualmente P.
Recuerda que en este caso el ángulo de desfase es 0 grados, ya que están en fase las dos ondas.
CIRCUITOS L
Son los circuitos que solo tienen componente inductivo (bobinas puras). En este caso la V y la I están desfasadas 90º.
La intensidad esta retrasada 90º respecto a la tensión o la tensión está adelantada 90º respecto a la intensidad.
En estos circuitos en lugar de R tenemos Xl, impedancia inductiva.
La Xl es algo así como la resistencia de la parte inductiva.
Para calcularla es importante un valor llamado inductancia (L) que solo poseen las bobinas puras.
L será la inductancia y se mide en henrios, al multiplicarla por w (frecuencia angular) nos dará la impedancia inductiva.

Si consideramos la XL como la resistencia (resistencia inductiva), aplicando la Ley de Ohm generalizada, los valores eficaces son:
I = V/wL e I V/Xl siendo Xl = w x L.
El valor de la tensión en cualquier momento (instantánea) sería:
v = Vo x sen wt ; donde Vo es el valor máximo de la tensión, w frecuencia angular y t el tiempo.
Para la intensidad instantánea recuerda que la I está retrasada 90º respecto a la tensión.
Si wt es el ángulo para la tensión, como la intensidad está retrasada 90º respecto a la tensión, tenemos que la intensidad instantánea será:
i = Io x seno (wt - 90º)
CIRCUITOS C
Este tipo de circuitos son los que solo tienen componentes capacitivos (condensadores puros).
En este caso la V y la I están desfasadas 90º negativos (la V está retrasada en lugar de adelantada con respecto a la I).
La Xc será la impedancia capacitiva, algo parecido a la resistencia de la parte capacitiva.

Los valores eficaces, considerando la resistencia Xc (resistencia capacitiva) y aplicando la ley de ohm generalizada son:
I = V/Xc e I = V/Xc; siendo Xc = 1/wC.
El valor de la tensión en cualquier momento sería:
v = Vo x sen wt ; donde Vo es el valor inicial de la tensión, w frecuencia angular y t el tiempo.
Igualmente la intensidad:
i = Io x seno (wt + 90º), recuerda que la I está adelantada 90º.
Si quieres saber todo sobre los condensadores te recomendamos este enlace: Condensador.
Ahora que ya sabemos como se resuelven los circuitos de corriente alterna con receptores puros, veamos como se resuelven cuando son una mezcla de varios puros.
En este caso tenemos varias posibilidades, RL, RC y RLC.
Recuerda los ángulos de desfase en cada caso.
Es mejor para los circuitos en serie recordar los ángulos de desfase tomando como referencia en 0º a la intensidad.
En ese caso mira como quedarían:

CIRCUITO RL EN SERIE

Por ser un circuito en serie, la intensidad por los 2 receptores serán las mismas, y las tensiones serán la suma de las 2 tensiones, pero OJO, suma vectorial porque recuerda que están desfasadas-.
Si consideramos que la intensidad está en ángulo 0, la tensión de la resistencia estará en fase, pero la de la bobina estará adelantada 90º respecto a la intensidad del circuito y por lo tanto 90º adelantada respecto a la tensión de la resistencia también.
Podríamos dibujar las 3 tensiones en lo que se llama el triángulo de tensiones:

De este triángulo podemos deducir muchas fórmulas, solo tenemos que aplicar trigonometria.
Si ahora dividimos todos los vectores del triángulo entre la intensidad, nos queda un triángulo semejante pero más pequeño, que será el llamado triángulo de impedancias.

Por trigonometría podemos deducir varias fórmulas de este triángulo, como puedes ver en la imagen.
Potencias en Corriente Alterna
¿Qué pasaría si en el triángulo de tensiones multiplicamos todas las tensiones por la intensidad?
Pues que tendríamos el llamado triángulo de potencias, un triángulo semejante al de tensiones pero con valores mayores de los vectores.

De este triángulo, igual que con los demás, podemos deducir varias fórmulas por trigonometría.
Pero lo que está claro es que en corriente alterna las potencias son 3 diferentes.
Potencia Activa Pa = V x I cose ρ ; esta es la única que da trabajo útil, la realmente transformada.
Se mide en Vatios (w). Es la tensión eficaz, por la intensidad eficaz, por el coseno del ángulo que forman.
Potencia Reactiva S = V x I seno ρ ; esta es como si fuera una potencia perdida, cuanto menor sea mejor.
Se mide en voltio amperios reactivos (VAR)
Potencia Aparente Q = V x I ; se mide en voltio amperios (VA).
En cuanto a las potencias en alterna no estudiaremos más porque se nos haría el tema excesivamente largo.
Si quieres ampliar vete a este enlace: Potencia Eléctrica, donde se explican más detalladamente todas las potencias incluidas las de alterna.
Veamos un ejercicio sencillo y muy típico de un motor de corriente alterna, circuito RL:

En la parte de abajo tienes un enlace a una página con muchos más ejercicios resueltos de corriente alterna.
El circuito RL tiene un componente resistivo y otro inductivo (R y L).
Podemos trabajar con números complejos para resolver estos circuitos, o con los triángulos que hemos visto hasta ahora por trigonometría.
Veamos cómo sería si la impedancia la tratáramos como un número complejo.
Como en el componente resistivo la i y la v están en fase, el ángulo de desfase depende de la cantidad de componente inductivo que tenga.
Z = R + Xlj , como Xl= w x L (frecuencia angular por inductancia) podemos decir también Z = R + (w x L) j
¿No sabes lo que es un número complejo?
No te preocupes, es muy fácil aprender a trabajar con ellos, y para estos circuitos nos facilita mucho el trabajo.
Un número complejo (Z) en los Circuitos Electricos, lo utilizamos para representar con el llamado triángulo de impedancias:
Z = R + Xj; fíjate que a la parte X del número complejo (representada en el triángulo como un cateto) se le pone un j para representar el número complejo.
Ya está, así de fácil es un número complejo, lo que realmente representa un número complejo es un triángulo (hipotenusa y sus dos catetos).
Sigamos con nuestro circuito.
En los circuitos de corriente alterna el número complejo representa la impedancia del circuito (hipotenusa, Z), la resistencia de la parte resistiva pura (cateto R) y la diferencia (resta vectorial) entre la impedancia inductiva y la capacitiva (X = Xl - Xc), esta última con la letra j.
A la X se le llama Reactancia.
En los circuitos RL no tenemos Xc, por lo que X sería igual a Xl, si tuviéramos Xc (parte capacitiva), X sería (Xl-Xc) una resta de los dos vectores, como en nuestro caso no tenemos Xc, entonces X = Xl.
Según este triángulo podemos convertir el número complejo en número natural con la siguiente fórmula (por Pitágoras):
Z2 = R2 + Xl2Podríamos despejar Z para calcularla.
La intensidad sería I = V / Z, que en instantánea quedaría:
i = (Vo x seno wt) / (R + wLj) en complejo. Podemos convertirlo en eficaz sustituyendo la Z por la raíz cuadrada de (R + wL).
Los valores eficaces serían V = I /Z o I = V/Z.
CIRCUITO RC
Este es igual solo que ahora tenemos Xc en lugar de Xl. Recuerda que Xc = 1/wC.
La intensidad será la misma en el circuito por estar los dos componentes en serie, pero la tensión será la suma.
La diferencia con el anterior es que la tensión del condensador estará retrasada 90º con respecto a la intensidad, no adelantada como con la bobina.
Tendremos los mismos triángulo, pero boca abajo.

Además, si trabajamos con números complejos tenemos: Xc = 1/(wCj) y por lo tanto Z = R + 1/(wCj) en numero complejo.
Pero si hacemos el triangulo de impedancias en este caso la Z en número natural sería:
Z2 = R2 + (1/(wC))2
Ves que es igual pero sustituyendo Xl por Xc que es 1/wC, en lugar de Xl que es wL.
Ahora vamos analizar los circuito RLC que son los más interesantes:
CIRCUITOS RLC
Son los circuitos más reales.

Fíjate que si te acostumbras hacer todo con los triángulos de impedancias, de tensiones y de potencias es mucho más fácil.


Para resolver los circuitos de corriente alterna en paralelo, basta con aplicar a los circuitos la ley de ohm generalizada y las leyes de kirchhoff.
Además recuerda que en paralelo la tensión aplicada a cada elemento del circuito (R, L o C) es la misma y la intensidad por cada uno de ellos es distinta, por lo que no hay triángulo de tensiones, hay triángulo de intensidades.
Todo esto lo veremos en esta otra web para no hacerlo muy extenso: Circuitos RLC en Paralelo.
Ahora deberías ir a ver los ejercicios resueltos de c.a.: Ejercicios Alterna
También te puede interesar conocer y aprender los Sistemas Trifásicos, ya que los aqui estudiados son monofásicos.
Por último te recomendamos si quieres aprender a resolver todo tipo de circuitos eléctricos de forma fácil, el siguiente libro: Libro Circuitos Eléctricos
Y Ahora también puedes hacer el curso en UDEMY para aprender a resolver circuitos de corriente contínua y si entras desde este enlace tendrás un descuento del 35% sobre el precio del curso:
https://www.udemy.com/course/circuitos-electricos-en-corriente-continua/?couponCode=9E773C2AD5BFB19CE634
OJO la promoción caduca
Si te ha gustado haz click en Compartir, Gracias:
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
TAMBIEN TE PUEDE INTERESAR
Ejercicios Alterna
Sistemas Trifásicos
Teorema de Thevenin y Norton
Factor de Potencia
Inductancia
Compensación Reactiva
Tipos de Conexiones Electricas
Corriente Electrica
Armónicos Eléctricos
Circuitos Electricos
Circuitos en Paralelo y en Serie
Leyes de Kirchhoff
Maquinas Electricas
Cosas Tecnologicas
Instalaciones en Viviendas
Rectificador de Media Onda
Triac
