DIVISOR DE TENSION
¿Qué es un Divisor de Tensión?
Un Divisor de Tensión o Divisor de Voltaje es un circuito que divide la tensión de entrada en el circuito en otras dos diferentes y más pequeñas de salida.
En electrónica y electricidad se usa para alimentar (proporcionar tensión de alimentación) a un aparato, con una tensión más pequeña que la que proporcionan las pilas o baterías disponibles (fuente de alimentación).
En definitiva sirve para obtener una tensión más pequeña partiendo de una tensión mayor.
Antes de seguir, recordarte que si quieres aprender electrónica de forma fácil para todos, te recomendamos el siguiente libro que contiene los conceptos básicos de electrónica explicados de forma sencilla y amena: Libro Electrónica Básica
Imagina que queremos alimentar una bombilla a 6V y solo disponemos de una pila de 10V.
¿Qué haremos?.
Pues la respuesta es muy sencilla: Un divisor de tensión que nos divida la tensión de 10 voltios de la pila (Ventrada) en dos, una de 6V (Vsalida) y otra de 4V.
También se utiliza mucho para resolver problemas más complejos y que en algunos sitios nos encontraremos que una parte del circuito es un divisor de tensión o un divisor de corriente.
Circuito Divisor de Tensión
El circuito es muy sencillo, solo necesitamos 2 resistencias y conectarlas en serie como en el siguiente circuito:
Como ves tenemos una entrada con una Ve (tensión de entrada) y una salida en la Resistencia Rs.
La R1 se usa para dividir la tensión de entrada en 2 tensiones en la zona de salida. Ventrada = V en R1 + V en Rs.
La fórmula general del divisor de tensión es:
Sabiendo los valores de las resistencias, podemos obtener directamente el valor de la tensión de salida.
Para obtener la fórmula es muy sencillo, solo tienes que hacer una simple regla de 3.
Cuando sacamos el circuito equivalente de las 2 resistencias en serie, tenemos que Rt es la suma de R1 + R2.
En esa Rt tenemos la tensión total, por lo que la tensión en una sola será la de la fórmula de la siguiente figura sacada de la regla de 3:
Si en R1 + R2 hay Vt
En R1 habrá V1; donde V1 será la incógnita de la regla de 3 y que tendremos que despejar.
Al margen de la fórmula general vista antes, la mejor forma de resolver estos circuitos es considerando que es un simple circuito de 2 resistencias en serie, donde se cumple:
Rt = R1 + Rs;
It = I1 = Is;
Ve = V1 + Vs;
Nota: Si no tienes claro los circuitos en serie, te recomendamos que antes vayas al siguiente enlace: Circuitos Serie y Paralelo.
Como sabemos que en serie la intensidad que circula por R1 será igual a la que circula por Rs tenemos:
I1 = V1/R1 e Is = Vs/Rs, entonces igualando:
V1/R1 = Vs/Rs;
¿Cuántos valores conocemos de esa ecuación?
Pues en nuestro ejemplo V1 que tendrá que asumir los 4V, Vs que tendrá que ser de 6V para conectar nuestra lámpara y Rs que será la resistencia de nuestro receptor a conectar a 6V, que mediremos de forma muy sencilla con el polímetro.
Tendremos que despejar el valor de R1 para construir correctamente nuestro divisor. Imagina que medimos con el polímetro y tenemos Rs = 450Ω
4/R1 = 6/
R1 = (V1 x Rs) / Vs = (4 x 450) /6 = 300Ω
Si ponemos una desasistencia de 300Ω en R1 podemos conectar nuestro receptor a 6V ¿Lo comprobamos?
Veamos como sería la Resistencia total: R1 + Rs = 300 + 450 = 750Ω
Veamos como sería la Intensidad Total It = 10/750 = 0,0133333A, recuerda este valor es igual a I1 = Is = It.
¿Cómo sería la tensión de salida en nuestro receptor?
Vs = Is x Rs = 0,0133333 x 450 = 6V
!!!Perfecto!!!
Ya tenemos nuestro divisor de tensión.
Si te fijas en el circuito de arriba del divisor de tensión, al lado del circuito, viene una fórmula.
Es una fórmula que se utiliza muchas veces en los divisores de tensión y que nos puede ser muy útil en algún momento.
Divisor de Voltaje con Potenciómetro
Una forma sencilla de construir un divisor de tensión que nos valga para varias tensiones de salida diferentes es simplemente poner un potenciómetro en donde colocábamos la R1:
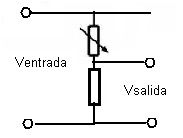
Recuerda: Un potenciómetro es una resistencia variable, por ejemplo entre 0 ohmios y 10.000 ohmios.
Para saber más vete al enlace: Potenciómetro.
Fíjate que ahora solo cambiando el valor del potenciómetro cambiaremos la tensión de salida.
Aumentando o disminuyendo la resistencia del potenciómetro, aumentaremos o disminuiremos la tensión de salida.
Ya tenemos nuestro divisor de tensión, que en estos casos se suelo llamar divisor de tensión variable o regulador de tensión.
¡OJO! un error común es pensar que a nuestro divisor de tensión le podemos acoplar a la Rs otro receptor en paralelo y que se mantenga la tensión de salida. ¡¡¡Esto no pasa!!! no es cierto.
Podríamos suponer que, por ejemplo, a la lámpara anterior que esta a 6V le podemos acoplar otro receptor y por estar en paralelo a la lámpara estaría conectado a 6V también.
Pero todo esto no es verdad. Todo cambia ya que ahora tenemos 3 resistencias, de las cuales 2 están en paralelo.
Este tipo de divisores suele llamarse divisores de tensión en carga.
Divisor de Tensión con Carga
¿Qué pasa cuando conectamos una carga nueva (bombilla, motor, etc.) en paralelo a la Rs anterior en el circuito.
Ahora tendremos una R1, una Rs y una R de carga o Load (RL).
Al conectar el nuevo receptor, este tendrá una resistencia (RL) y el problema es que esta resistencia "chupará" una intensidad que hará cambiarla I total del circuito, ya no será la I teórica calculada anteriormente.
Además la I de la RL depende de su valor, lo que el valor de la Itotal ahora también va a depender del valor de esta RL.
Si cambia la intensidad total del circuito, las caídas de tensión en R1 (la V1) y en Rs (Vs) también cambiarán, ya que dependen de la Itotal.
Ahora los valores de Vs del ejercicio en vacío ya no serán los 6V que realmente necesitamos.
En este tipo de divisores lo que se calcula es la tensión a la que quedarán realmente conectados nuestros receptores Rs y RL, que será la tensión de salida y si que serán iguales las dos, pero no del mismo valor que si solo estuviera Rs.
Para esto lo mejor es resolver el circuito considerando que es un circuito mixto de resistencias.
Primero calculamos la resistencia equivalente de la rama en paralelo, y luego tendremos un simple circuito de 2 resistencias en serie.
Recuerda que la resistencia equivalente de una rama de resistencias en paralelo es:
Una vez calculada la equivalente de Rs y RL ya tenemos un circuito igual al de vacío con 2 resistencias, R1 y REquivalente.
Ahora con la tensión total y la Rt podemos calcular la It y con esa intensidad calcular la tensión real en Rs que será igual que en RL.
Nuestro problema será calcular la Tensión en la RL que es la que necesitamos para conectar nuestro receptor a una tensión determinada, y recuerda que la RL será la misma que la que obtengamos al calcular la tensión en la Requivalente, ya que están en paralelo.
Fíjate la diferencia entre uno y otro:
Si quieres aprender a resolver circuitos mixtos: Circuitos Mixtos Eléctricos.
Solución Práctica Rápida Para Construir un Divisor de Tensión en Carga
En muchas ocasiones, para calcular un divisor de tensión en carga que nos ofrezca una tensión de salida concreta para conectar un receptor determinado, lo que se suele hacer una solución práctica muy sencilla que vamos a ver a continuación, y que tiene un pequeño margen de error, pero que en la mayoría de las veces no tiene importancia.
La solución práctica es calcular primero la corriente que va a demandar nuestro receptor, por ejemplo una bombilla, y hacer los cálculos para el divisor en vacío, pero para una corriente 10 veces mayor.
La pila de 10V sería la entrada (Ventrada) y la bombilla funcionará a 6 V.
La bombilla la colocaríamos en la tensión de salida (Vsalida).
Lógicamente tenemos que conocer la intensidad que demandará nuestro aparato al conectarlo para que funcione correctamente.
En nuestro caso la bombilla imaginemos que tiene una intensidad de 1mA (miliamperio) = 0,001A.
Datos iniciales: Ve, Vs, e Intensidad que consume el aparato de salida (en nuestro caso la bombilla)
A veces no nos dan el valor directamente de la intensidad, pero si no es así, nos darán la potencia del aparato. Imagina que nuestra bombilla es de 0,006w.
¿Cual será su intensidad?.
Sabiendo la fórmula de la potencia es muy fácil calcular la intensidad, ya que sabemos la tensión a la que estará conectada, en nuestro caso a 6V:
Potencia = V x I; despejando I = P/V. En nuestro caso I = 0,006w/6 = 0,001A = 1mA
Una vez que conocemos la intensidad que consume nuestro receptor, hacemos los cálculos del divisor del tensión en vació pero para una supuesta intensidad 10 veces mayor, es decir para una I de 0,001 x10 = 0,01A.
Ya tenemos los datos iniciales. Ve = 10V; Vs = 6V; I = 0,01A.
Ahora veamos como construimos el divisor de tensión.
El problema es saber de que valor tendrían que ser las resistencias para que con 10V a la entrada obtengamos 6V a la salida con una intensidad de 0,01A. OJO estos 3 datos son siempre imprescindibles.
Es muy fácil, solo hay que aplicar la ley de ohm en cada resistencia.
V1 = R1 x I; despejamos R1;
R1 = V1/I = 4/0,01 = 400Ω
de la misma forma Vs = Rs x I;
despejando Rs = Vs / I = 6/0,01 = 600Ω
Si montamos nuestro divisor con esas dos resistencias, problema solucionado.
Comprobemos que es cierto.
¿Qué tensión tendremos en Rs?
Apliquemos la ley de ohm: Vs = Rs x I = 600Ω x 0,01A = 6V. ¡¡¡Perfecto!!!
En V1 tendremos V1 = R1 x I = 400 x 0,01 = 4V
¿Qué pasará ahora cuando conectemos nuestro receptor (bombilla)?
Ahora aunque conectemos la bombilla a la salida, como el divisor está calculado para intensidades muy superiores, la intensidad que aumenta la total teórica del circuito en vacío es la de la bombilla 0,001A.
Este aumento de intensidad no cambiará mucho los valores de V1 y Vs por que es muy pequeña (10 veces menor) respecto a la que circulaba en vacío, no produciendo grandes cambios.
Para acabar decir que es mucho mejor utilizar el divisor de tensión en vacío (el primero estudiado) o incluso mejor aún construir el divisor de tensión con el polímetro.
Quiero acabar recomendandote el mejor libro para aprender la resolución de circuitos eléctricos:
Y si lo que quieres es aprender electrónica digital de forma fácil para todos, te recomendamos el siguiente libro:
Si te ha gustado haz clic en Compartir, Gracias:
Recuerda, Si quieres aprender electrónica de forma fácil para todos, te recomendamos el siguiente libro que contiene los conceptos básicos de electrónica explicados de forma sencilla y amena: Libro Electrónica Básica
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
Un Divisor de Tensión o Divisor de Voltaje es un circuito que divide la tensión de entrada en el circuito en otras dos diferentes y más pequeñas de salida.
En electrónica y electricidad se usa para alimentar (proporcionar tensión de alimentación) a un aparato, con una tensión más pequeña que la que proporcionan las pilas o baterías disponibles (fuente de alimentación).
En definitiva sirve para obtener una tensión más pequeña partiendo de una tensión mayor.
Antes de seguir, recordarte que si quieres aprender electrónica de forma fácil para todos, te recomendamos el siguiente libro que contiene los conceptos básicos de electrónica explicados de forma sencilla y amena: Libro Electrónica Básica
Imagina que queremos alimentar una bombilla a 6V y solo disponemos de una pila de 10V.
¿Qué haremos?.
Pues la respuesta es muy sencilla: Un divisor de tensión que nos divida la tensión de 10 voltios de la pila (Ventrada) en dos, una de 6V (Vsalida) y otra de 4V.
También se utiliza mucho para resolver problemas más complejos y que en algunos sitios nos encontraremos que una parte del circuito es un divisor de tensión o un divisor de corriente.
Circuito Divisor de Tensión
El circuito es muy sencillo, solo necesitamos 2 resistencias y conectarlas en serie como en el siguiente circuito:
Como ves tenemos una entrada con una Ve (tensión de entrada) y una salida en la Resistencia Rs.
La R1 se usa para dividir la tensión de entrada en 2 tensiones en la zona de salida. Ventrada = V en R1 + V en Rs.
La fórmula general del divisor de tensión es:
Sabiendo los valores de las resistencias, podemos obtener directamente el valor de la tensión de salida.
Para obtener la fórmula es muy sencillo, solo tienes que hacer una simple regla de 3.
Cuando sacamos el circuito equivalente de las 2 resistencias en serie, tenemos que Rt es la suma de R1 + R2.
En esa Rt tenemos la tensión total, por lo que la tensión en una sola será la de la fórmula de la siguiente figura sacada de la regla de 3:
Si en R1 + R2 hay Vt
En R1 habrá V1; donde V1 será la incógnita de la regla de 3 y que tendremos que despejar.
Al margen de la fórmula general vista antes, la mejor forma de resolver estos circuitos es considerando que es un simple circuito de 2 resistencias en serie, donde se cumple:
Rt = R1 + Rs;
It = I1 = Is;
Ve = V1 + Vs;
Nota: Si no tienes claro los circuitos en serie, te recomendamos que antes vayas al siguiente enlace: Circuitos Serie y Paralelo.
Como sabemos que en serie la intensidad que circula por R1 será igual a la que circula por Rs tenemos:
I1 = V1/R1 e Is = Vs/Rs, entonces igualando:
V1/R1 = Vs/Rs;
¿Cuántos valores conocemos de esa ecuación?
Pues en nuestro ejemplo V1 que tendrá que asumir los 4V, Vs que tendrá que ser de 6V para conectar nuestra lámpara y Rs que será la resistencia de nuestro receptor a conectar a 6V, que mediremos de forma muy sencilla con el polímetro.
Tendremos que despejar el valor de R1 para construir correctamente nuestro divisor. Imagina que medimos con el polímetro y tenemos Rs = 450Ω
4/R1 = 6/
R1 = (V1 x Rs) / Vs = (4 x 450) /6 = 300Ω
Si ponemos una desasistencia de 300Ω en R1 podemos conectar nuestro receptor a 6V ¿Lo comprobamos?
Veamos como sería la Resistencia total: R1 + Rs = 300 + 450 = 750Ω
Veamos como sería la Intensidad Total It = 10/750 = 0,0133333A, recuerda este valor es igual a I1 = Is = It.
¿Cómo sería la tensión de salida en nuestro receptor?
Vs = Is x Rs = 0,0133333 x 450 = 6V
!!!Perfecto!!!
Ya tenemos nuestro divisor de tensión.
Si te fijas en el circuito de arriba del divisor de tensión, al lado del circuito, viene una fórmula.
Es una fórmula que se utiliza muchas veces en los divisores de tensión y que nos puede ser muy útil en algún momento.
Divisor de Voltaje con Potenciómetro
Una forma sencilla de construir un divisor de tensión que nos valga para varias tensiones de salida diferentes es simplemente poner un potenciómetro en donde colocábamos la R1:
Recuerda: Un potenciómetro es una resistencia variable, por ejemplo entre 0 ohmios y 10.000 ohmios.
Para saber más vete al enlace: Potenciómetro.
Fíjate que ahora solo cambiando el valor del potenciómetro cambiaremos la tensión de salida.
Aumentando o disminuyendo la resistencia del potenciómetro, aumentaremos o disminuiremos la tensión de salida.
Ya tenemos nuestro divisor de tensión, que en estos casos se suelo llamar divisor de tensión variable o regulador de tensión.
¡OJO! un error común es pensar que a nuestro divisor de tensión le podemos acoplar a la Rs otro receptor en paralelo y que se mantenga la tensión de salida. ¡¡¡Esto no pasa!!! no es cierto.
Podríamos suponer que, por ejemplo, a la lámpara anterior que esta a 6V le podemos acoplar otro receptor y por estar en paralelo a la lámpara estaría conectado a 6V también.
Pero todo esto no es verdad. Todo cambia ya que ahora tenemos 3 resistencias, de las cuales 2 están en paralelo.
Este tipo de divisores suele llamarse divisores de tensión en carga.
Divisor de Tensión con Carga
¿Qué pasa cuando conectamos una carga nueva (bombilla, motor, etc.) en paralelo a la Rs anterior en el circuito.
Ahora tendremos una R1, una Rs y una R de carga o Load (RL).
Al conectar el nuevo receptor, este tendrá una resistencia (RL) y el problema es que esta resistencia "chupará" una intensidad que hará cambiarla I total del circuito, ya no será la I teórica calculada anteriormente.
Además la I de la RL depende de su valor, lo que el valor de la Itotal ahora también va a depender del valor de esta RL.
Si cambia la intensidad total del circuito, las caídas de tensión en R1 (la V1) y en Rs (Vs) también cambiarán, ya que dependen de la Itotal.
Ahora los valores de Vs del ejercicio en vacío ya no serán los 6V que realmente necesitamos.
En este tipo de divisores lo que se calcula es la tensión a la que quedarán realmente conectados nuestros receptores Rs y RL, que será la tensión de salida y si que serán iguales las dos, pero no del mismo valor que si solo estuviera Rs.
Para esto lo mejor es resolver el circuito considerando que es un circuito mixto de resistencias.
Primero calculamos la resistencia equivalente de la rama en paralelo, y luego tendremos un simple circuito de 2 resistencias en serie.
Recuerda que la resistencia equivalente de una rama de resistencias en paralelo es:
Una vez calculada la equivalente de Rs y RL ya tenemos un circuito igual al de vacío con 2 resistencias, R1 y REquivalente.
Ahora con la tensión total y la Rt podemos calcular la It y con esa intensidad calcular la tensión real en Rs que será igual que en RL.
Nuestro problema será calcular la Tensión en la RL que es la que necesitamos para conectar nuestro receptor a una tensión determinada, y recuerda que la RL será la misma que la que obtengamos al calcular la tensión en la Requivalente, ya que están en paralelo.
Fíjate la diferencia entre uno y otro:
Si quieres aprender a resolver circuitos mixtos: Circuitos Mixtos Eléctricos.
Solución Práctica Rápida Para Construir un Divisor de Tensión en Carga
En muchas ocasiones, para calcular un divisor de tensión en carga que nos ofrezca una tensión de salida concreta para conectar un receptor determinado, lo que se suele hacer una solución práctica muy sencilla que vamos a ver a continuación, y que tiene un pequeño margen de error, pero que en la mayoría de las veces no tiene importancia.
La solución práctica es calcular primero la corriente que va a demandar nuestro receptor, por ejemplo una bombilla, y hacer los cálculos para el divisor en vacío, pero para una corriente 10 veces mayor.
La pila de 10V sería la entrada (Ventrada) y la bombilla funcionará a 6 V.
La bombilla la colocaríamos en la tensión de salida (Vsalida).
Lógicamente tenemos que conocer la intensidad que demandará nuestro aparato al conectarlo para que funcione correctamente.
En nuestro caso la bombilla imaginemos que tiene una intensidad de 1mA (miliamperio) = 0,001A.
Datos iniciales: Ve, Vs, e Intensidad que consume el aparato de salida (en nuestro caso la bombilla)
A veces no nos dan el valor directamente de la intensidad, pero si no es así, nos darán la potencia del aparato. Imagina que nuestra bombilla es de 0,006w.
¿Cual será su intensidad?.
Sabiendo la fórmula de la potencia es muy fácil calcular la intensidad, ya que sabemos la tensión a la que estará conectada, en nuestro caso a 6V:
Potencia = V x I; despejando I = P/V. En nuestro caso I = 0,006w/6 = 0,001A = 1mA
Una vez que conocemos la intensidad que consume nuestro receptor, hacemos los cálculos del divisor del tensión en vació pero para una supuesta intensidad 10 veces mayor, es decir para una I de 0,001 x10 = 0,01A.
Ya tenemos los datos iniciales. Ve = 10V; Vs = 6V; I = 0,01A.
Ahora veamos como construimos el divisor de tensión.
El problema es saber de que valor tendrían que ser las resistencias para que con 10V a la entrada obtengamos 6V a la salida con una intensidad de 0,01A. OJO estos 3 datos son siempre imprescindibles.
Es muy fácil, solo hay que aplicar la ley de ohm en cada resistencia.
V1 = R1 x I; despejamos R1;
R1 = V1/I = 4/0,01 = 400Ω
de la misma forma Vs = Rs x I;
despejando Rs = Vs / I = 6/0,01 = 600Ω
Si montamos nuestro divisor con esas dos resistencias, problema solucionado.
Comprobemos que es cierto.
¿Qué tensión tendremos en Rs?
Apliquemos la ley de ohm: Vs = Rs x I = 600Ω x 0,01A = 6V. ¡¡¡Perfecto!!!
En V1 tendremos V1 = R1 x I = 400 x 0,01 = 4V
¿Qué pasará ahora cuando conectemos nuestro receptor (bombilla)?
Ahora aunque conectemos la bombilla a la salida, como el divisor está calculado para intensidades muy superiores, la intensidad que aumenta la total teórica del circuito en vacío es la de la bombilla 0,001A.
Este aumento de intensidad no cambiará mucho los valores de V1 y Vs por que es muy pequeña (10 veces menor) respecto a la que circulaba en vacío, no produciendo grandes cambios.
Para acabar decir que es mucho mejor utilizar el divisor de tensión en vacío (el primero estudiado) o incluso mejor aún construir el divisor de tensión con el polímetro.
Quiero acabar recomendandote el mejor libro para aprender la resolución de circuitos eléctricos:
Y si lo que quieres es aprender electrónica digital de forma fácil para todos, te recomendamos el siguiente libro:
Si te ha gustado haz clic en Compartir, Gracias:
Recuerda, Si quieres aprender electrónica de forma fácil para todos, te recomendamos el siguiente libro que contiene los conceptos básicos de electrónica explicados de forma sencilla y amena: Libro Electrónica Básica
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
TAMBIEN TE PUEDE INTERESAR
Divisor de Corriente
Electronica Basica
Sobretensiones
Teorema de Thevenin y Norton
Magnitudes Electricas
Potenciometro
Varistor
Leyes de Kirchhoff
Diodo Zener
Fuente de Alimentacion
Resistencia Electrica
Voltimetro
