SISTEMA DIEDRICO

Vamos a estudiar una introducción sencilla al sistema diedrico.

El sistema diédrico es un método gráfico el cual consiste en obtener la imagen de un objeto (en planta y alzado), mediante la proyección de haces (rayos) proyectantes perpendiculares a dos planos principales de proyección.

plano horizontal (PH) y plano vertical (PV).

El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar.

A estas dos proyecciones se les suele llamar en el dibujo técnico Alzado y Planta. La tercera vista, la vista lateral se llamaría Perfíl.



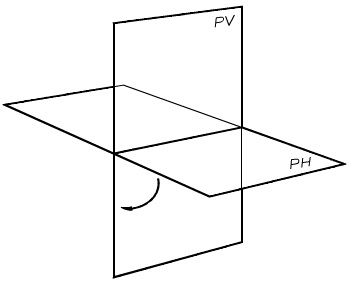
Representación de un Punto

Un punto situado en el espacio se representa mediante sus dos proyecciones (a modo de sombras) sobre los planos principales: proyección horizontal y proyección vertical.

Cota
Se denomina cota de un punto del espacio a la distancia entre él y su proyección en el plano horizontal, o lo que es lo mismo la distancia entre la proyección vertical y la línea de Tierra (LT).

Alejamiento
Se denomina alejamiento de un punto del espacio a la distancia entre el y su proyección en el plano vertical, o lo que es lo mismo a la distancia entre la proyección horizontal y la línea de Tierra (LT).

Vamos a representar un punto. Lo primero es que para dibujar sus dos proyecciones sobre los planos en un papel tendremos que abatir (abrir) los dos planos para que nos quede en dos dimensiones (las que tiene el papel) y luego dibujar sus proyecciones sobre los planos.

En la figura tenemos el punto colocado en el espacio sobre los dos planos y a la derecha vemos la representación sobre el papel.



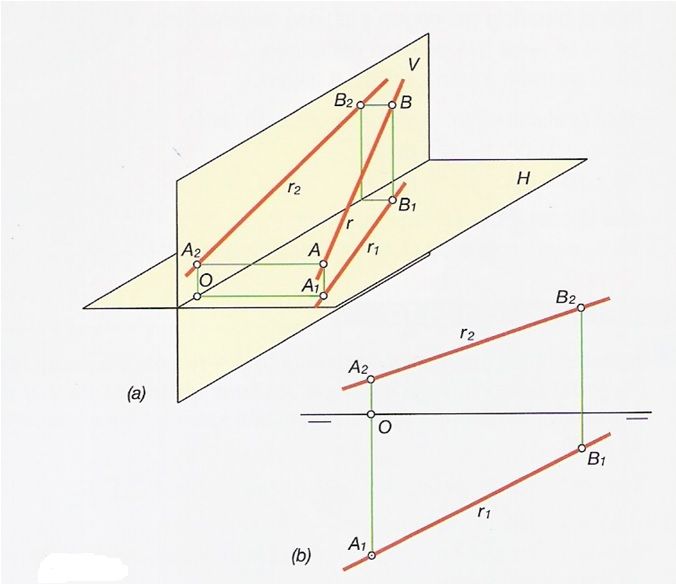
Representación de Una Recta

Una recta está definida cuando se conocen sus dos proyecciones, horizontal y vertical. La proyección de una recta sobre un plano es otra recta, formada por la proyección de todos los puntos de ella.

Conociendo las parejas de proyecciones (sobre el plano vertical y sobre el horizontal) de dos puntos de una recta, se obtiene la proyección uniendo los dos puntos.

Fíjate en la figura hemos cogido dos puntos cualquiera de la recta A y B para sacar sus proyecciones.

En la parte de abajo sería como se dibujaría en el papel la recta, mediante sus proyecciones.



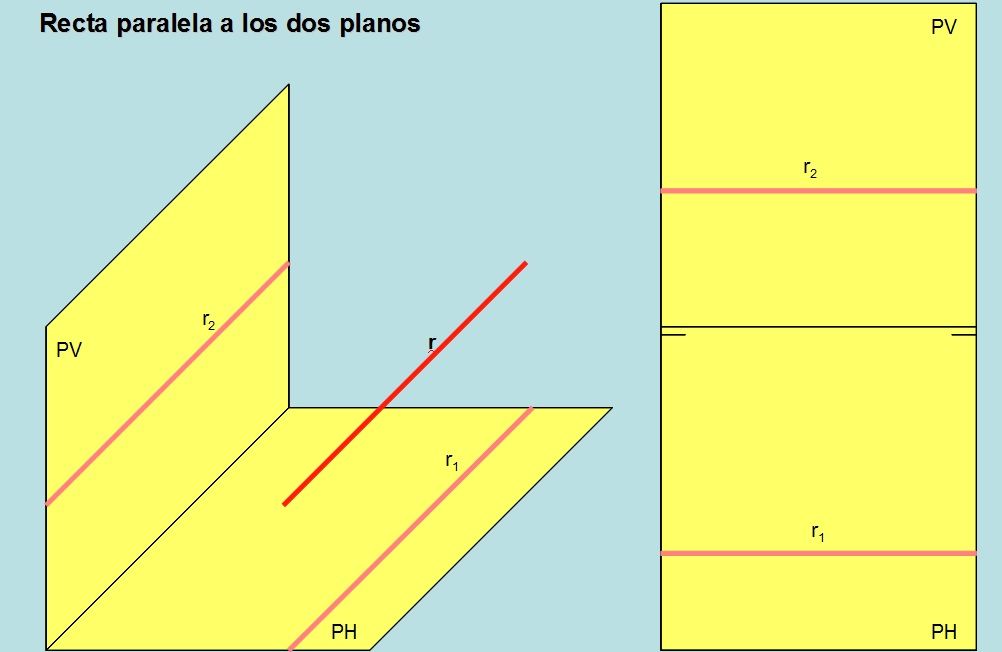
Veamos como sería una recta paralela a los dos planos:



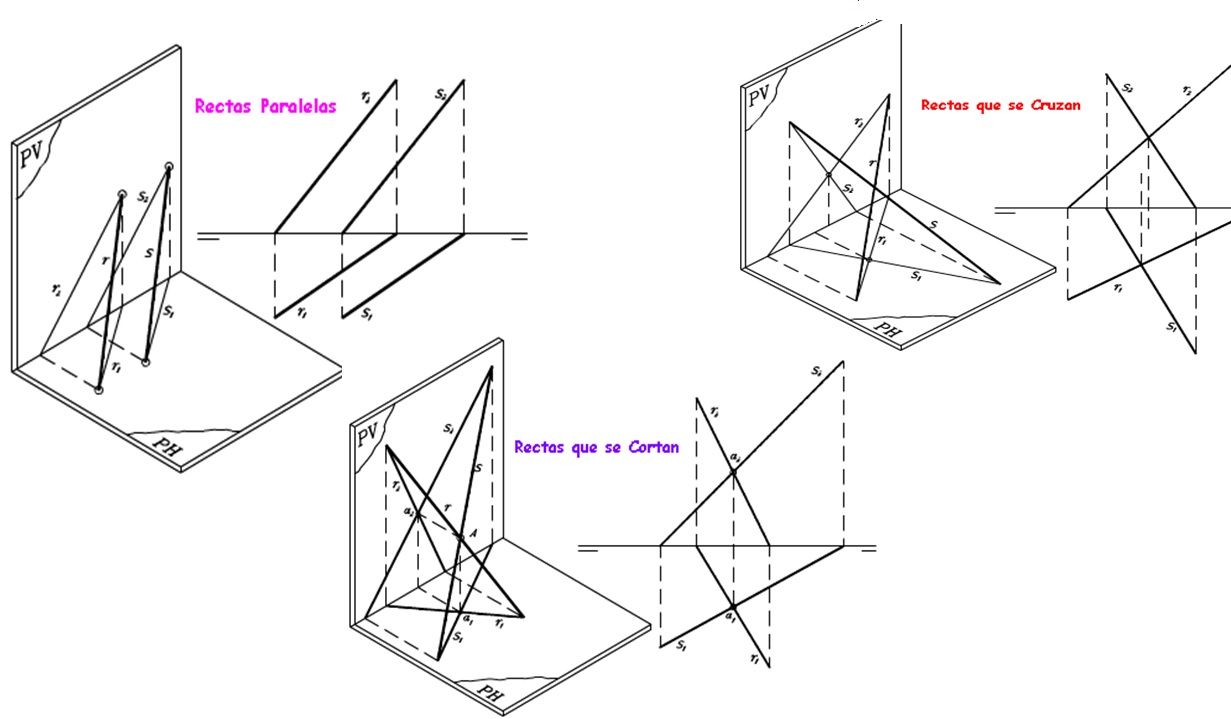
Ahora veamos dos rectas en diferentes posiciones y su representaciones:


Representación de Un Plano

Hasta ahora hemos aprendido los conceptos y procedimientos para determinar las proyecciones diédricas de un punto y una recta; y aunque hemos nombrado algunas veces al plano, solamente ha sido para referirnos a los de proyección.

Generalmente entendemos que una superficie plana es aquella que puede contener una recta imaginaria en cualquier dirección.

La definición anterior la podemos aplicar a la hora de referirnos a un plano en el sistema diédrico.

Así pues, las caras de una forma, objeto, poliedro, etc., son planos delimitados por aristas (rectas) y vértices (puntos).

En el sistema diédrico entendemos que un plano es una superficie plana infinita e ilimitada.

Para definir un plano necesitamos los siguientes elementos geométricos: tres puntos cualesquiera que no estén alineados, una recta y un punto exterior a ella, dos rectas que se cortan y dos rectas paralelas.

Un plano se representa mediante sus trazas. Las Trazas de un plano son las rectas intersección del plano con los planos de proyección.



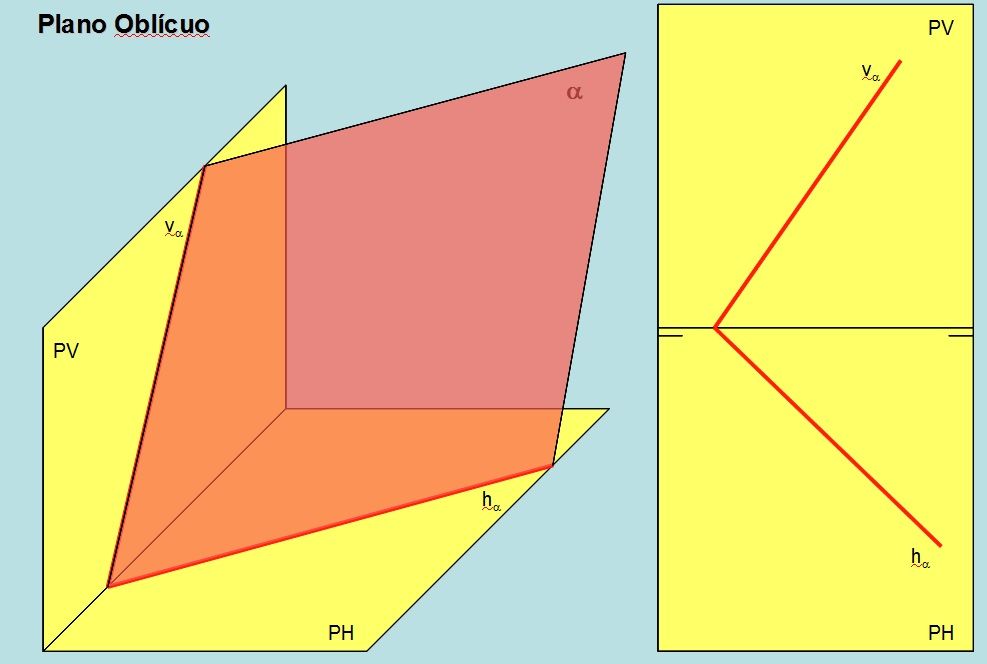
Veamos situaciones de planos en sistema diedrico diferentes.



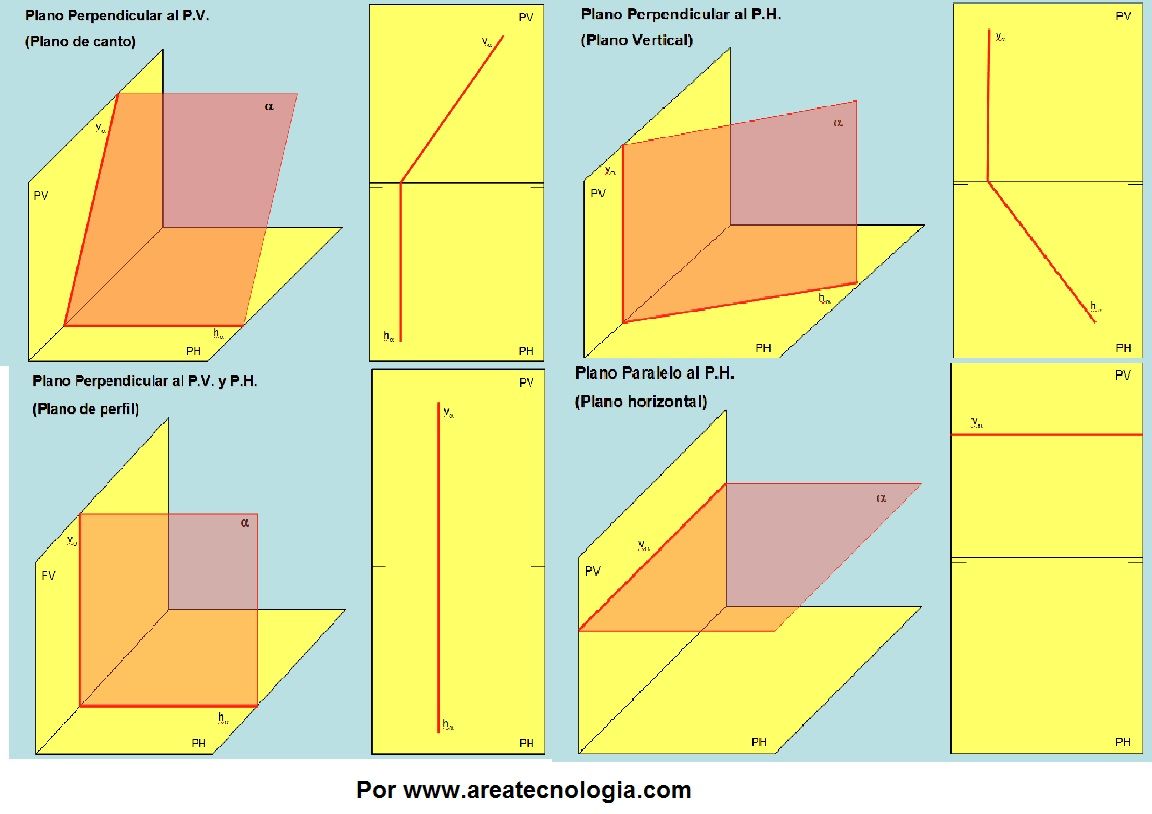
En la siguiente presentación os dejamos más sobre diedrico con ejercicios resueltos para que veas como se representan más rectas y planos en diedrico.



Y en este video explica el sistema diedrico desde cero.



Si te ha gustado haz click en Me Gusta, Gracias:

© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.